Beyond and Within EDA: Taking EDA into Modelling

Beyond and Within EDA

Introduction

This blog is the continuation of the previous blog post A General Way of Doing EDA. Please follow that before reading this blog.

Once we got the knowledge of the data like its properties and features, we can move ahead by taking that knowledge to make some sort of inference. Its often called Modelling. Sometimes Feature Engineerig is also done within EDA and beyond it. Feature engineering is very crucial part of Modelling and it is very important to understand the data and its properties before we can make any kind of inference. Lets take few example of the scenarios and see how we can make some kind of inference from it:

• In a supermarket data, we knew via EDA that there seems to be high number of sweets purchase during December month and we want to take this insight into action by preserving more sweet varieties in the store so that we wont be out of stocks. Here one will take business action.
• Lets suppose we took some action (like advertised hugely and preserved stock) in above case and we want to see its out come. But how do we see the outcome before it actually happened? Well, in that case we will be predicting the sales based upon the previous year’s data. Here one will take inference action.
• Lets suppose a CEO of a Fintech company wants to maximize the profit by giving loans to many customers as much as possible. There is a huge financial risk. Here, they might need to make few clusters of the customers based on their income, job history and balance history. Here they will try to make cluster and make distinct services focusing on each. Will they take loan or not? This might be a classification problem and if they do, how much are they going to take? It is regression problem.

The cases can be infinite but one always have to ask how feasible and logical will it be?

But our focus in this blog is on the second part, how do we utilize the information, insights found from the EDA to maximize our profit or knowledge base. In the previous blog, we knew several facts about the data and we found clear cluster of the field data based on the device’s place and does it make sense? Yes of course because each device was on distinctly different places. We have 3 devices with below environmental conditions:

device	environmental conditions
00:0f:00:70:91:0a	stable conditions, cooler and more humid
1c:bf:ce:15:ec:4d	highly variable temperature and humidity
b8:27:eb:bf:9d:51	stable conditions, warmer and dryer

What we Knew from EDA?

• We did ANOVA test to claim that, there is significant difference in field values read by each device.
• From Correlation, we knew that few fields have huge correlation for device placed on distinct place. For example, there was high correlation between time and smoke, then CO for device at stable and warmer place.
• LPG, Smoke, CO have high correlation between other features. And so on.

Reading Data

Just like previous time, lets read data from local storage and perform some preliminary tasks.

import autoviz
from autoviz.AutoViz_Class import AutoViz_Class
from pandas_profiling import ProfileReport
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from datetime import datetime
import warnings
from plotly.offline import init_notebook_mode, iplot
import plotly.figure_factory as ff
import cufflinks
import plotly.io as pio 
import matplotlib as mpl

cufflinks.go_offline()
cufflinks.set_config_file(world_readable=True, theme='pearl')
pio.renderers.default = "notebook" # should change by looking into pio.renderers
sns.set()
pd.options.display.max_columns = None
mpl.rcParams['agg.path.chunksize'] = 10000
%matplotlib inline

df=pd.read_csv("iot_telemetry_data.csv")


df["date"]= df.ts.apply(datetime.fromtimestamp)

d={"00:0f:00:70:91:0a":"cooler,more,humid", 
   "1c:bf:ce:15:ec:4d":"variable temp/humidity",
   "b8:27:eb:bf:9d:51":"stable, warmer, dry"}
df["device_name"] = df.device.apply(lambda x: d[x])
df

	ts	device	co	humidity	light	lpg	motion	smoke	temp	date	device_name
0	1.594512e+09	b8:27:eb:bf:9d:51	0.004956	51.000000	False	0.007651	False	0.020411	22.700000	2020-07-12 05:46:34.385975	stable, warmer, dry
1	1.594512e+09	00:0f:00:70:91:0a	0.002840	76.000000	False	0.005114	False	0.013275	19.700001	2020-07-12 05:46:34.735568	cooler,more,humid
2	1.594512e+09	b8:27:eb:bf:9d:51	0.004976	50.900000	False	0.007673	False	0.020475	22.600000	2020-07-12 05:46:38.073573	stable, warmer, dry
3	1.594512e+09	1c:bf:ce:15:ec:4d	0.004403	76.800003	True	0.007023	False	0.018628	27.000000	2020-07-12 05:46:39.589146	variable temp/humidity
4	1.594512e+09	b8:27:eb:bf:9d:51	0.004967	50.900000	False	0.007664	False	0.020448	22.600000	2020-07-12 05:46:41.761235	stable, warmer, dry
...	...	...	...	...	...	...	...	...	...	...	...
405179	1.595203e+09	00:0f:00:70:91:0a	0.003745	75.300003	False	0.006247	False	0.016437	19.200001	2020-07-20 05:48:33.162015	cooler,more,humid
405180	1.595203e+09	b8:27:eb:bf:9d:51	0.005882	48.500000	False	0.008660	False	0.023301	22.200000	2020-07-20 05:48:33.576561	stable, warmer, dry
405181	1.595203e+09	1c:bf:ce:15:ec:4d	0.004540	75.699997	True	0.007181	False	0.019076	26.600000	2020-07-20 05:48:36.167959	variable temp/humidity
405182	1.595203e+09	00:0f:00:70:91:0a	0.003745	75.300003	False	0.006247	False	0.016437	19.200001	2020-07-20 05:48:36.979522	cooler,more,humid
405183	1.595203e+09	b8:27:eb:bf:9d:51	0.005914	48.400000	False	0.008695	False	0.023400	22.200000	2020-07-20 05:48:37.264313	stable, warmer, dry

405184 rows × 11 columns

Clustering

Clustering is a kind of unsupervised algorithm where we try to group data points into number of cluster based on its feature. There is one clustering algorithm which is supervised and it is called KNN (K Nearest Neighbor).

There are several clustering algorithm and some we are going to cover in this blog are:

1. K Means Clustering
2. K Medoid Clustering

K Means Clustering

Algorithm

Let $P = {p_1,p_2,p_3,…,p_n}$ be the set of data points and $C = {c_1,c_2,c_3,…,c_n}$ be the set of centers.

1. Step 1: Initially randomly select appropriate numbers of “c” cluster center.
2. Step 2: Calculate distance between each data point $P = {p_1,p_2,p_3,…,p_n}$ and cluster center ‘c’.
3. Step 3: Keep data points to the cluster center whose distance from the cluster center is minimum of all the cluster centers. Here we calculate the distance using euclidean distance. Mathematically, $ = \sum_{i=1}^n (x_i^2-y_i^2) $
4. Step 4: Now, recalculate the new cluster center using $ \frac{1}{c}\sum_{i=1}^c x_i $ where $c_i$ represent the number of data point in $i^th$ clusters.
5. Step 5: Again calculate the distance between new cluster centers and each data points.
6. Step 6: If number of data points in a cluster are updated then repeat step 3 otherwise terminate.

For our experiment, lets select two fields and try to make cluster out of it. We will choose co and temp and try to make cluster with them. We already know how many clusters could there be but still lets explore.

We will use KMeans from sklearn.

from sklearn.cluster import KMeans

cols = ["co", "humidity", "light", "motion", "smoke", "temp"]
cols = ["co", "temp"]
X = df[cols]

kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

df["cluster"]=y_kmeans
X["cluster"] = y_kmeans

df 

	ts	device	co	humidity	light	lpg	motion	smoke	temp	date	device_name	cluster
0	1.594512e+09	b8:27:eb:bf:9d:51	0.004956	51.000000	False	0.007651	False	0.020411	22.700000	2020-07-12 05:46:34.385975	stable, warmer, dry	2
1	1.594512e+09	00:0f:00:70:91:0a	0.002840	76.000000	False	0.005114	False	0.013275	19.700001	2020-07-12 05:46:34.735568	cooler,more,humid	0
2	1.594512e+09	b8:27:eb:bf:9d:51	0.004976	50.900000	False	0.007673	False	0.020475	22.600000	2020-07-12 05:46:38.073573	stable, warmer, dry	2
3	1.594512e+09	1c:bf:ce:15:ec:4d	0.004403	76.800003	True	0.007023	False	0.018628	27.000000	2020-07-12 05:46:39.589146	variable temp/humidity	1
4	1.594512e+09	b8:27:eb:bf:9d:51	0.004967	50.900000	False	0.007664	False	0.020448	22.600000	2020-07-12 05:46:41.761235	stable, warmer, dry	2
...	...	...	...	...	...	...	...	...	...	...	...	...
405179	1.595203e+09	00:0f:00:70:91:0a	0.003745	75.300003	False	0.006247	False	0.016437	19.200001	2020-07-20 05:48:33.162015	cooler,more,humid	0
405180	1.595203e+09	b8:27:eb:bf:9d:51	0.005882	48.500000	False	0.008660	False	0.023301	22.200000	2020-07-20 05:48:33.576561	stable, warmer, dry	2
405181	1.595203e+09	1c:bf:ce:15:ec:4d	0.004540	75.699997	True	0.007181	False	0.019076	26.600000	2020-07-20 05:48:36.167959	variable temp/humidity	1
405182	1.595203e+09	00:0f:00:70:91:0a	0.003745	75.300003	False	0.006247	False	0.016437	19.200001	2020-07-20 05:48:36.979522	cooler,more,humid	0
405183	1.595203e+09	b8:27:eb:bf:9d:51	0.005914	48.400000	False	0.008695	False	0.023400	22.200000	2020-07-20 05:48:37.264313	stable, warmer, dry	2

405184 rows × 12 columns

set(y_kmeans)

{0, 1, 2}

Lets plot the result in scatterplot and to do so, lets make our own plotting function which we might be using many times. Please refer to the docstring for more info.

def scatterplot(data,x,y,hue,figsize=(15,10), title=None, extra=[]):
    """
        data: Dataframe 
        x: field name to plot on x axis
        y: field name to plot on y axis
        hue: hue value to see distinct color for each hue
        figsize: size of our plot
        title: title of our plot
        extra: if we want to plot other thing which might not be necessary
    """
    fig = plt.figure(figsize=figsize)
    sns.scatterplot(data=data, x=x, y=y, hue=hue)
    #sns.relplot(data=data, x=x, y=y, hue=hue, sizes=figsize)    
    if len(extra)>0:
        plt.scatter(extra[0], extra[1], c='black', s=200, alpha=0.5);
    if not title:
        title = f"{x} vs {y} vs {hue}"
    plt.title(label=title, fontsize=25)
    plt.xlabel(x,fontsize=20)
    plt.ylabel(y,fontsize=20)
    plt.legend(fontsize=20).set_title(title=hue)
    plt.show()

scatterplot(X, cols[0], cols[1],"cluster")

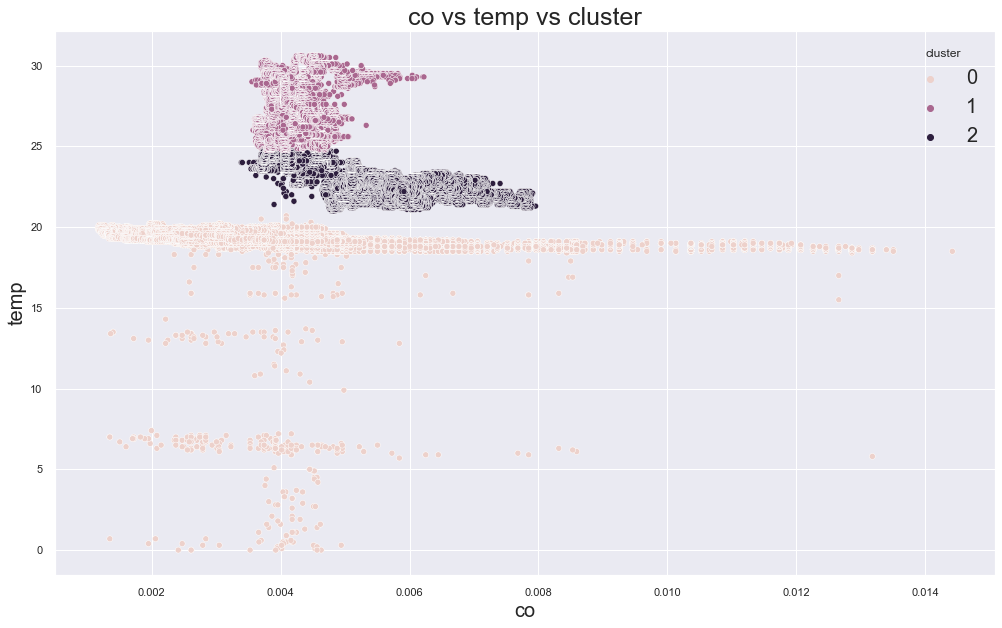
There seems to be having some sort of cluster but is that meaningful? Lets view that:

df.groupby("cluster").device_name.value_counts()

cluster  device_name           
0        cooler,more,humid         111815
         variable temp/humidity       100
1        variable temp/humidity     74012
2        stable, warmer, dry       187451
         variable temp/humidity     31806
Name: device_name, dtype: int64

As we can see on above value counts, the device_name variable temp/humidity is on all 3 clusters and it is clear that we were unable to make distinct meaningful clusters. So lets try something new, how about finding number of optimal clusters? We will loop through number of Ks and find the best one based on the value of error.

cols = ["co", "temp"]
X = df[cols]
errors = []
cs=range(2,10)
for c in cs:
    kmeans = KMeans(n_clusters=c)
    kmeans.fit(X)
    y_kmeans = kmeans.predict(X)
    
    print(kmeans.inertia_)
    
    errors.append(kmeans.inertia_)
    
    df["cluster"]=y_kmeans
    X["cluster"] = y_kmeans
    scatterplot(X, cols[0], cols[1],"cluster")
    print(df.groupby("cluster").device_name.value_counts())

1055305.0183423792

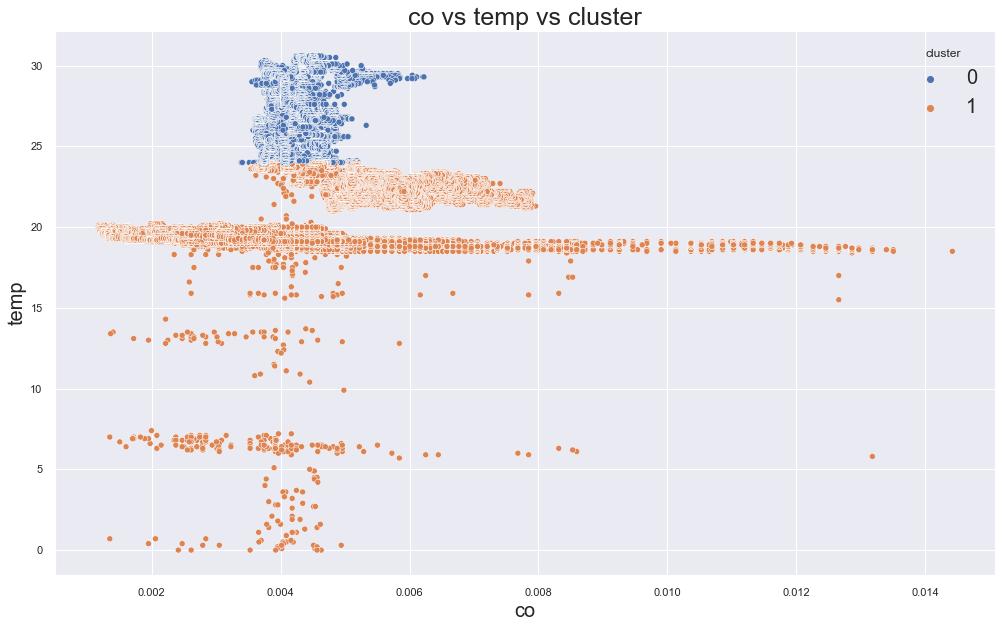
cluster  device_name           
0        variable temp/humidity     85759
         stable, warmer, dry          213
1        stable, warmer, dry       187238
         cooler,more,humid         111815
         variable temp/humidity     20159
Name: device_name, dtype: int64
359294.69291916804

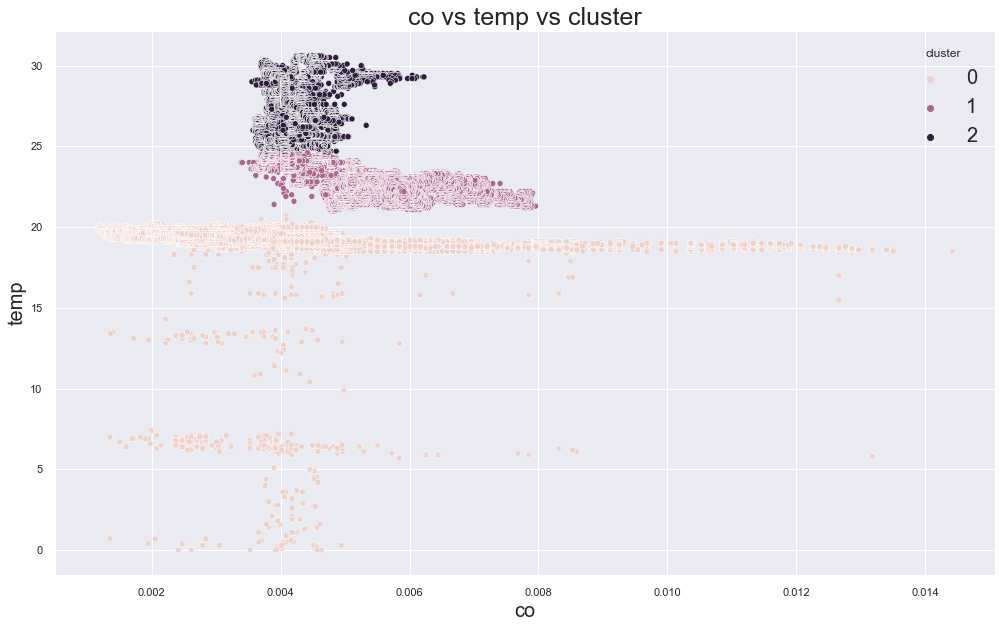
cluster  device_name           
0        cooler,more,humid         111815
         variable temp/humidity       100
1        stable, warmer, dry       187451
         variable temp/humidity     30352
2        variable temp/humidity     75466
Name: device_name, dtype: int64
214028.3487953433

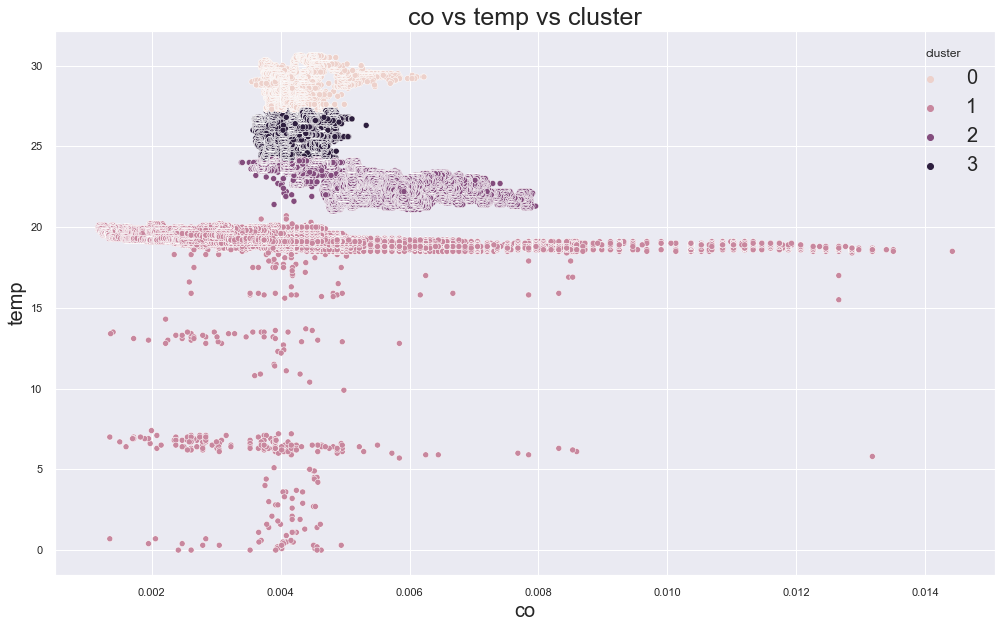
cluster  device_name           
0        variable temp/humidity     27625
1        cooler,more,humid         111815
         variable temp/humidity       100
2        stable, warmer, dry       187451
         variable temp/humidity     24943
3        variable temp/humidity     53250
Name: device_name, dtype: int64
151700.8705451637

cluster  device_name           
0        cooler,more,humid         111815
         variable temp/humidity       100
1        variable temp/humidity     27625
2        stable, warmer, dry        41022
         variable temp/humidity     25828
3        variable temp/humidity     51736
4        stable, warmer, dry       146429
         variable temp/humidity       629
Name: device_name, dtype: int64
102536.81251504176

cluster  device_name           
0        variable temp/humidity     51736
1        cooler,more,humid         111646
         variable temp/humidity        28
2        stable, warmer, dry       146429
         variable temp/humidity       629
3        variable temp/humidity     27625
4        stable, warmer, dry        41022
         variable temp/humidity     25828
5        cooler,more,humid            169
         variable temp/humidity        72
Name: device_name, dtype: int64
81340.56487052461

cluster  device_name           
0        stable, warmer, dry       146429
         variable temp/humidity       629
1        variable temp/humidity     27625
2        variable temp/humidity     25407
3        cooler,more,humid         111646
         variable temp/humidity        28
4        stable, warmer, dry        41022
         variable temp/humidity     25828
5        cooler,more,humid            169
         variable temp/humidity        72
6        variable temp/humidity     26329
Name: device_name, dtype: int64
66498.23856232288

cluster  device_name           
0        stable, warmer, dry        41022
         variable temp/humidity     25828
1        stable, warmer, dry       146429
         variable temp/humidity       629
2        cooler,more,humid         111646
         variable temp/humidity        28
3        variable temp/humidity     15260
4        variable temp/humidity     26329
5        variable temp/humidity     25407
6        cooler,more,humid            169
         variable temp/humidity        72
7        variable temp/humidity     12365
Name: device_name, dtype: int64
53887.02544998735

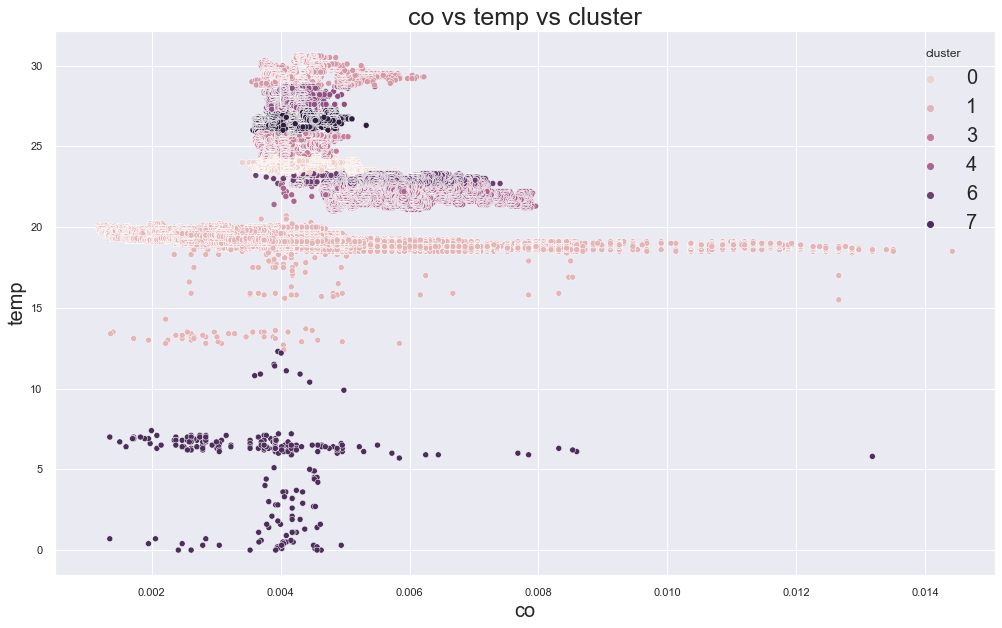
cluster  device_name           
0        variable temp/humidity     22853
         stable, warmer, dry         2619
1        cooler,more,humid         111646
         variable temp/humidity        28
2        variable temp/humidity     12365
3        variable temp/humidity     25407
4        stable, warmer, dry       146429
         variable temp/humidity       629
5        variable temp/humidity     15260
6        stable, warmer, dry        38403
         variable temp/humidity      2975
7        cooler,more,humid            169
         variable temp/humidity        72
8        variable temp/humidity     26329
Name: device_name, dtype: int64

plt.figure(figsize=(15,10))
plt.plot(cs,errors,'bx-')
plt.xlabel('Values of K') 
plt.ylabel('Sum of squared distances/Inertia') 
plt.title('Elbow Method For Optimal k')
plt.show()

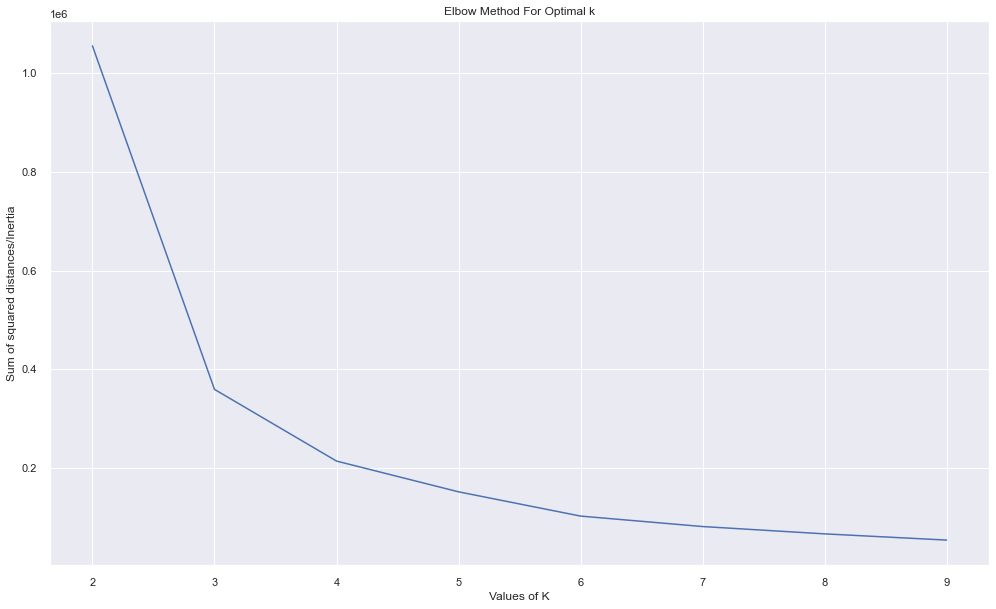
Looking over the plot above, the best K value seems to be 3 or 4 from where the errors has fallen hugely. But the data points are not correctly clustered.

K Medoids Clustering

Please fllow this blog of ours to learn about K-Medoids Clustering from Scratch.

K-medoids are a prominent clustering algorithm as an improvement of the predecessor, K-Means algorithm. Despite its widely used and less sensitive to noises and outliers, the performance of K-medoids clustering algorithm is affected by the distance function. From here.

When k-means algorithm is not appropriate to make a objects of cluster to the data points then k-medoid clustering algorithm is prefer. The medoid is objects of cluster whose dissimilarity to all the objects in the cluster is minimum. The main difference between K-means and K-medoid algorithm that we work with arbitrary matrix of distance instead of euclidean distance. K-medoid is a classical partitioning technique of clustering that cluster the dataset into k cluster. It is more robust to noise and outliers because it may minimize sum of pair-wise dissimilarities however k-means minimize sum of squared Euclidean distances. Most common distances used in KMedoids clustering techniques are Manhattan distance or Minkowski distance and here we will use Manhattan distance.

Manhattan Distance

Of p1, p2 is: $

(x2-x1)+(y2-y1)

$.

Algorithm

• Step 1: Randomly select(without replacement) k of the n data points as the median.
• Step 2: Associate each data points to the closest median.
• Step 3: While the cost of the configuration decreases:
  • For each medoid m, for each non-medoid data point o:
    • Swap m and o, re-compute the cost.
    • If the total cost of the configuration increased in the previous step, undo the swap.

We will use scikit learn extra instead of scikit learn this provides more features of algorithms than sklearn. But there is huge problem with KMedoids which is the time and memory complexity. We will be looping through data in big O. So we will try to cluster on sample data instead of the original data.

from sklearn_extra.cluster import KMedoids

cols = ["co", "temp"]
X = df[cols]
errors = []
cs=range(2,10)
for c in cs:
    kmedoids = KMedoids(n_clusters=c)
    kmedoids.fit(X.sample(10000))
    y_kmedoids = kmedoids.predict(X)
    
    print(kmedoids.inertia_)
    
    errors.append(kmedoids.inertia_)
    
    df["cluster"]=y_kmedoids
    X["cluster"] = y_kmedoids
    scatterplot(X, cols[0], cols[1],"cluster", title=f"{c} cluster and {cols[0]} vs {cols[1]} vs cluster")
    print(df.groupby("cluster").device_name.value_counts())

12166.707891029588

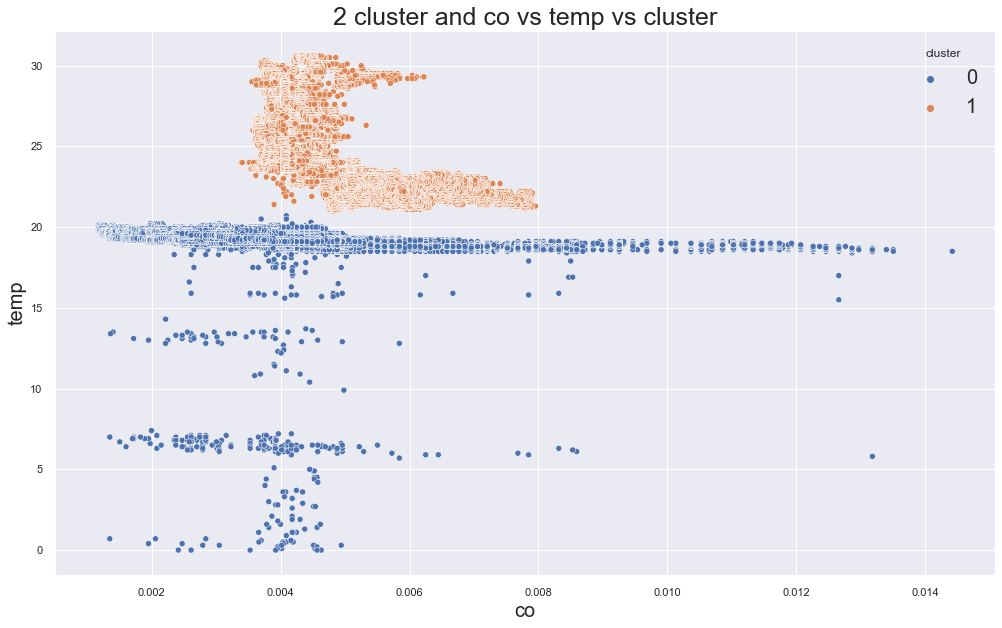
cluster  device_name           
0        cooler,more,humid         111815
         variable temp/humidity       100
1        stable, warmer, dry       187451
         variable temp/humidity    105818
Name: device_name, dtype: int64
6257.743841331246

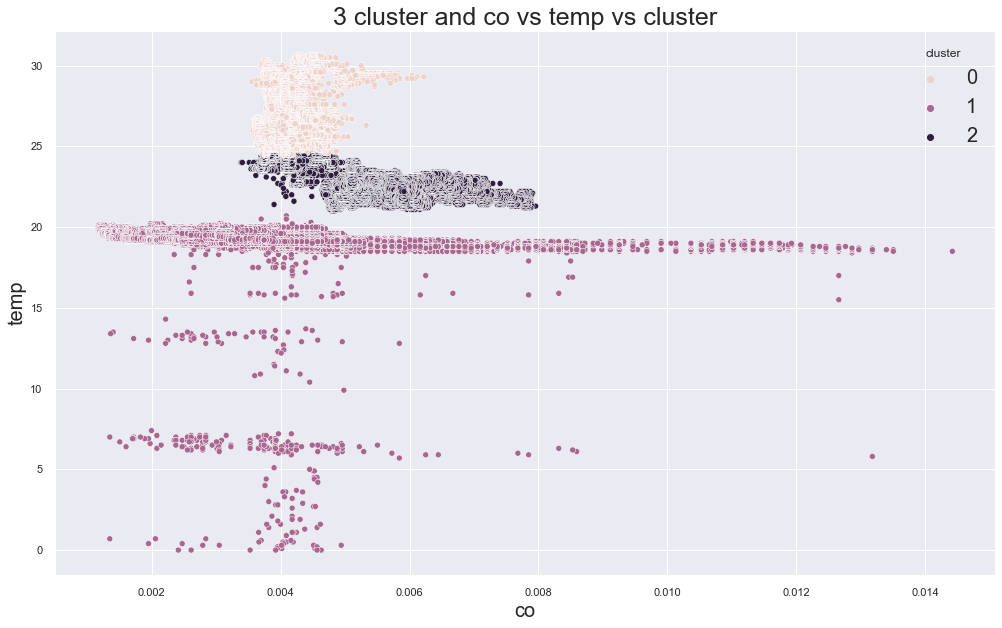
cluster  device_name           
0        variable temp/humidity     78090
1        cooler,more,humid         111815
         variable temp/humidity       100
2        stable, warmer, dry       187451
         variable temp/humidity     27728
Name: device_name, dtype: int64
5285.978025282497

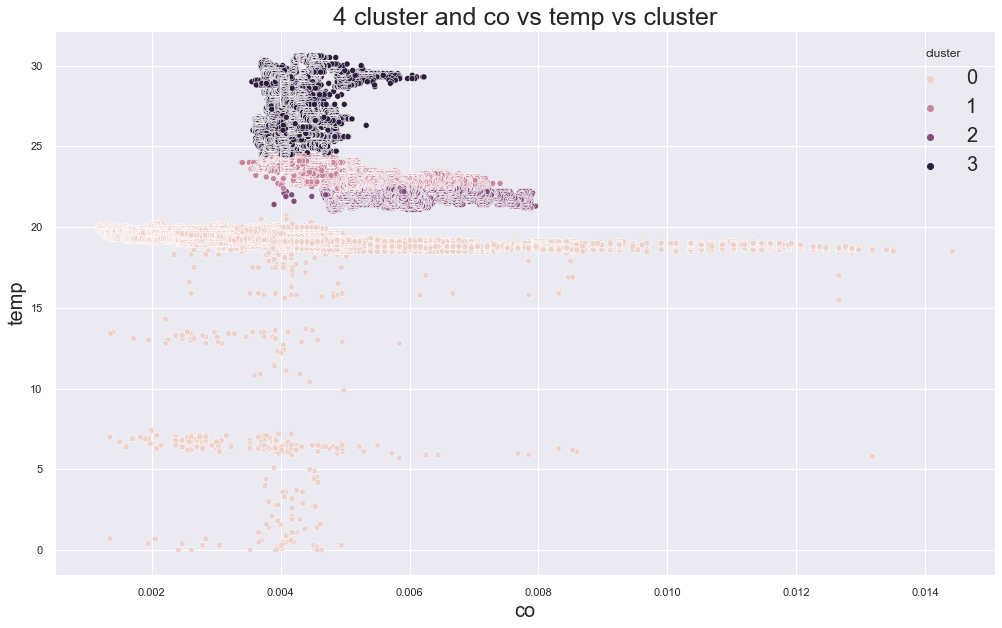
cluster  device_name           
0        cooler,more,humid         111815
         variable temp/humidity       100
1        stable, warmer, dry        72347
         variable temp/humidity     27619
2        stable, warmer, dry       115104
         variable temp/humidity       109
3        variable temp/humidity     78090
Name: device_name, dtype: int64
4796.422019787171

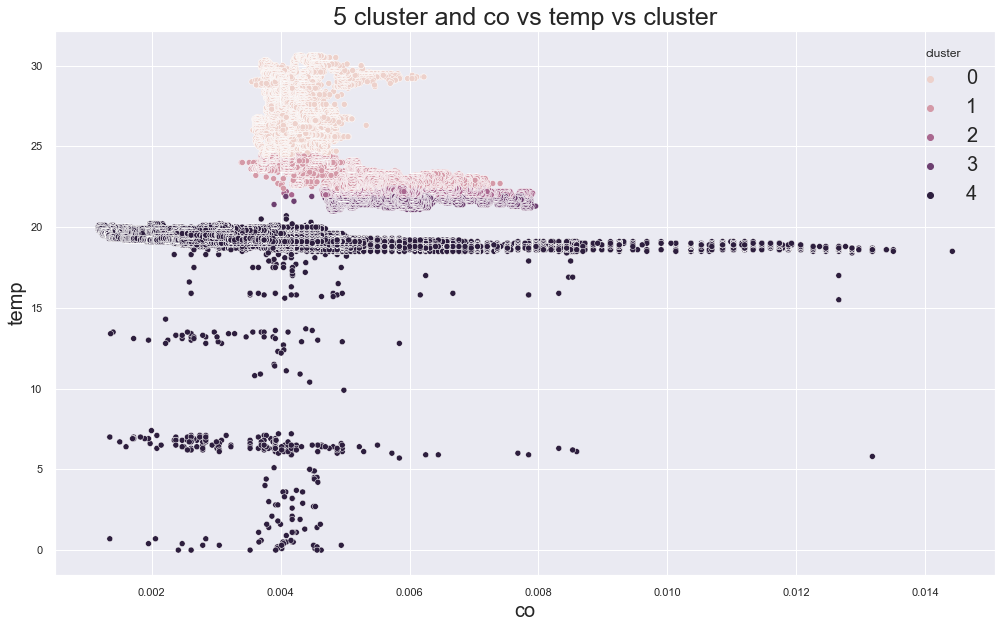
cluster  device_name           
0        variable temp/humidity     78090
1        stable, warmer, dry        72347
         variable temp/humidity     27619
2        stable, warmer, dry        67271
         variable temp/humidity       103
3        stable, warmer, dry        47833
         variable temp/humidity         6
4        cooler,more,humid         111815
         variable temp/humidity       100
Name: device_name, dtype: int64
4825.803826784304

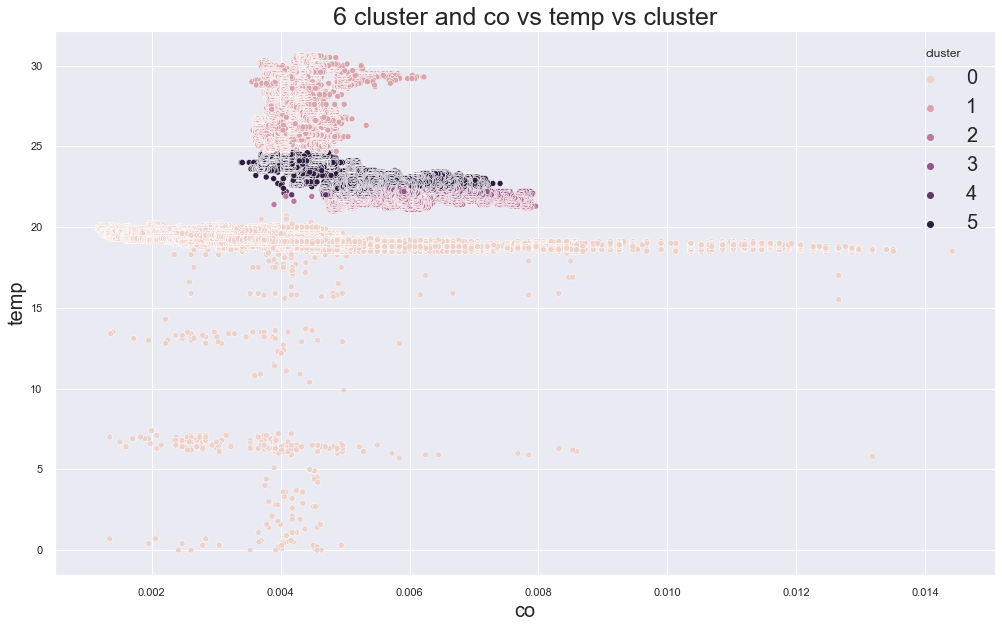
cluster  device_name           
0        cooler,more,humid         111815
         variable temp/humidity       100
1        variable temp/humidity     75466
2        stable, warmer, dry        47833
         variable temp/humidity         6
3        stable, warmer, dry        43309
         variable temp/humidity         1
4        stable, warmer, dry        23962
         variable temp/humidity       102
5        stable, warmer, dry        72347
         variable temp/humidity     30243
Name: device_name, dtype: int64
5244.391828106972

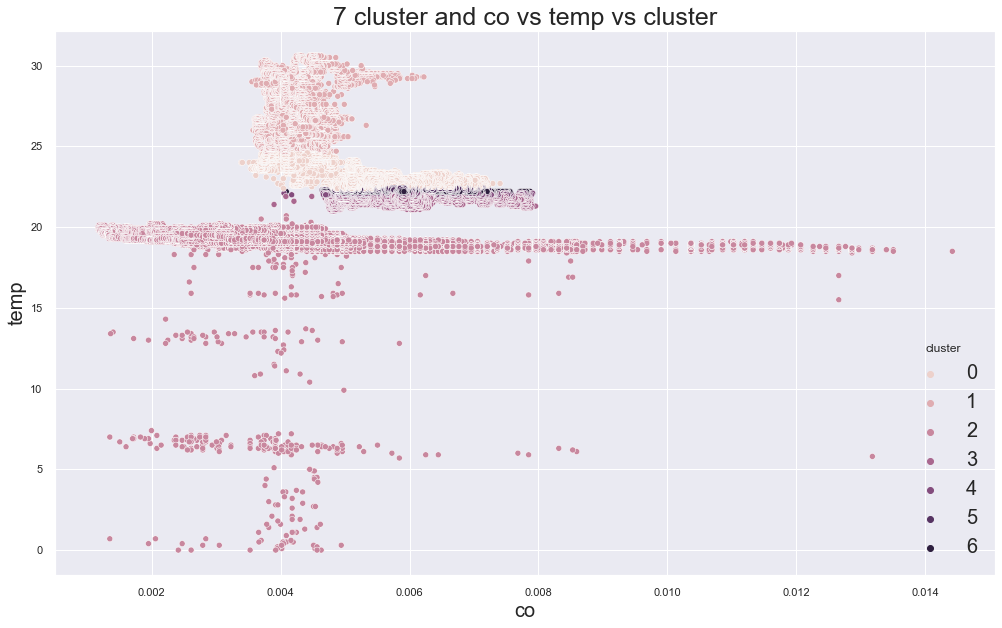
cluster  device_name           
0        stable, warmer, dry        72347
         variable temp/humidity     30243
1        variable temp/humidity     75466
2        cooler,more,humid         111815
         variable temp/humidity       100
3        stable, warmer, dry        47833
         variable temp/humidity         6
4        stable, warmer, dry        26271
         variable temp/humidity         2
5        stable, warmer, dry        24214
         variable temp/humidity       100
6        stable, warmer, dry        16786
         variable temp/humidity         1
Name: device_name, dtype: int64
9591.672713432437

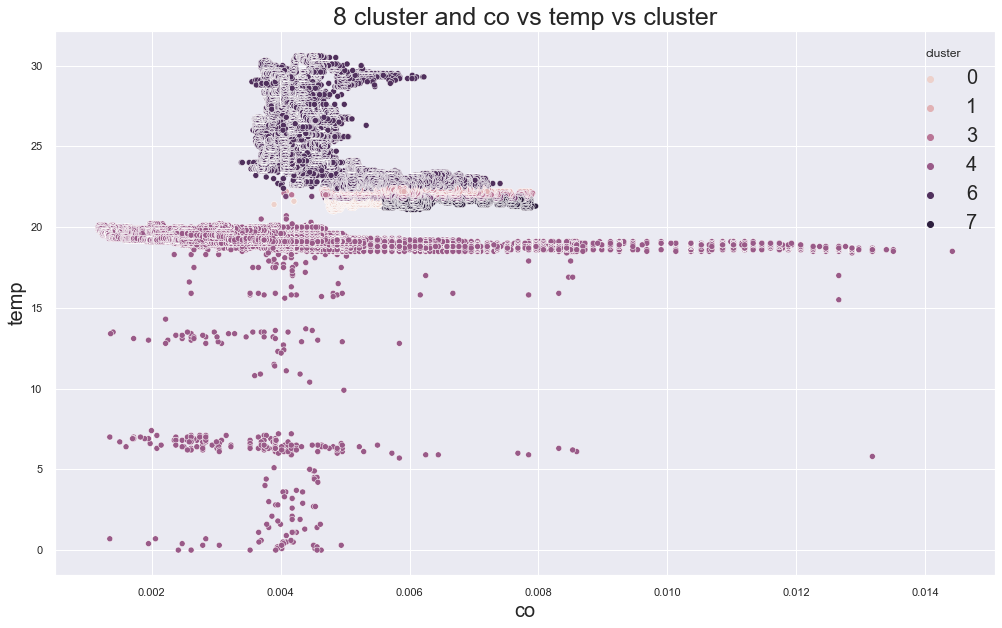
cluster  device_name           
0        stable, warmer, dry        15865
         variable temp/humidity         3
1        stable, warmer, dry        16786
         variable temp/humidity         1
2        stable, warmer, dry        24214
         variable temp/humidity       100
3        stable, warmer, dry        26271
         variable temp/humidity         2
4        cooler,more,humid         111815
         variable temp/humidity       100
5        stable, warmer, dry        20048
         variable temp/humidity         3
6        variable temp/humidity    105709
         stable, warmer, dry        72347
7        stable, warmer, dry        11920
Name: device_name, dtype: int64
5639.374780166998

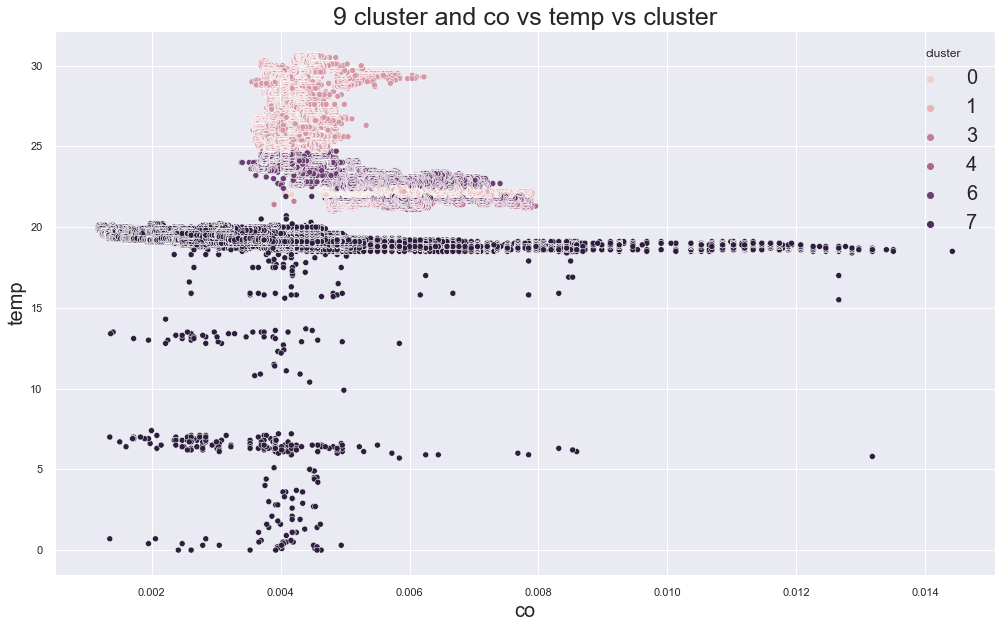
cluster  device_name           
0        stable, warmer, dry        24013
         variable temp/humidity       103
1        stable, warmer, dry        43258
2        variable temp/humidity     74012
3        stable, warmer, dry        15865
         variable temp/humidity         3
4        stable, warmer, dry         7457
5        stable, warmer, dry         4463
6        stable, warmer, dry        72347
         variable temp/humidity     31697
7        stable, warmer, dry        20048
         variable temp/humidity         3
8        cooler,more,humid         111815
         variable temp/humidity       100
Name: device_name, dtype: int64

plt.figure(figsize=(15,10))
plt.plot(cs,errors,'bx-')
plt.xlabel('Values of K') 
plt.ylabel('Sum of squared distances/Inertia') 
plt.title('Elbow Method For Optimal k')
plt.show()

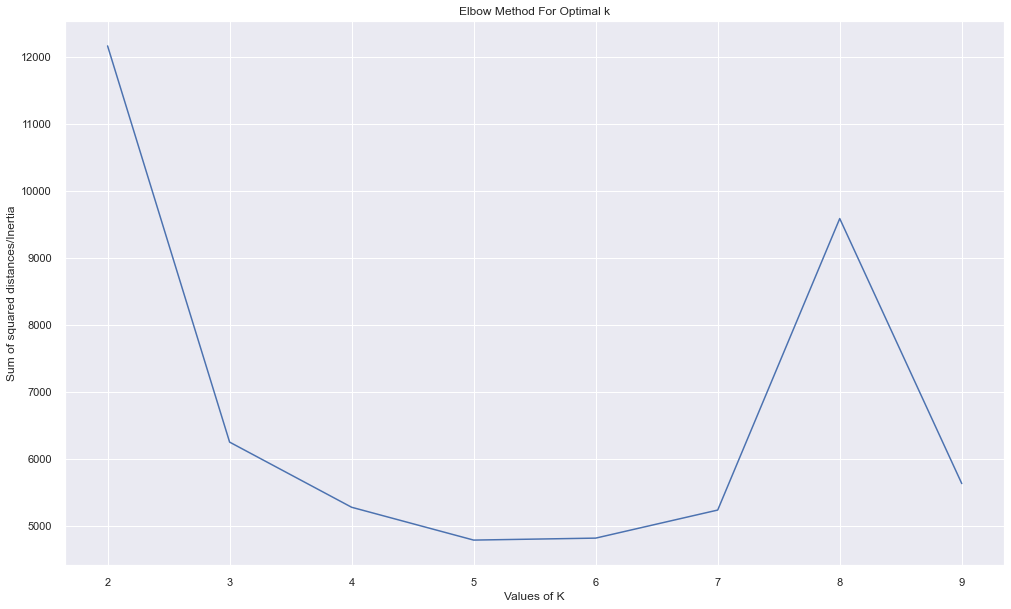
It looks that the best number of cluster is 3. But we were unable to cluster them properly.

There are several clustering algorithms available on the sklearn please follow them here.

Regression

Regression is a concept where we try to predict some values based on some parameters. Components in regression:

• Dependent Variables: Those variables whose value depends on some other value.
• Independent Variables:Those variables whose value does not depend on some other value.
• Parameters: Those variables whose value defines the relationship between dependent and independent variables.
• Error: How far is the predicted value from the actual value?

Linear Regression

Linear as name suggests is a regression where we try to fit linear relationship between two or more variables. A simple example of linear relationship or equation can be defined as:

Simple Linear Regression

\(y=mx+c\)

Where,

• y is dependent variable
• x is independent variable
• c is y intercept
• m is slope

Training or fitting a model in machine learning means finding those values which could give us as similar values as possible with the true label.

We have seen on the previous EDA part that there was some relationship between LPG, CO and Smoke and now in this part we will try to predict the value of CO based on LPG and Smoke.

from sklearn.linear_model import LinearRegression


X = df["lpg"].to_numpy().reshape(-1,1)
y = df["co"].to_numpy().reshape(-1,1)

model = LinearRegression()

model.fit(X, y)

pred = model.predict(X)

print(f"Y intercept: {model.intercept_}, Slope: {model.coef_}")

Y intercept: [-0.00160889], Slope: [[0.86328922]]

plt.figure(figsize=(15,10))
plt.scatter(X,y, color="r")
plt.plot(X,pred)
plt.xlabel("LPG")
plt.ylabel("CO")
plt.title("LPG vs CO prediction and original")
plt.legend(["Original", "Predicted"])
plt.show()

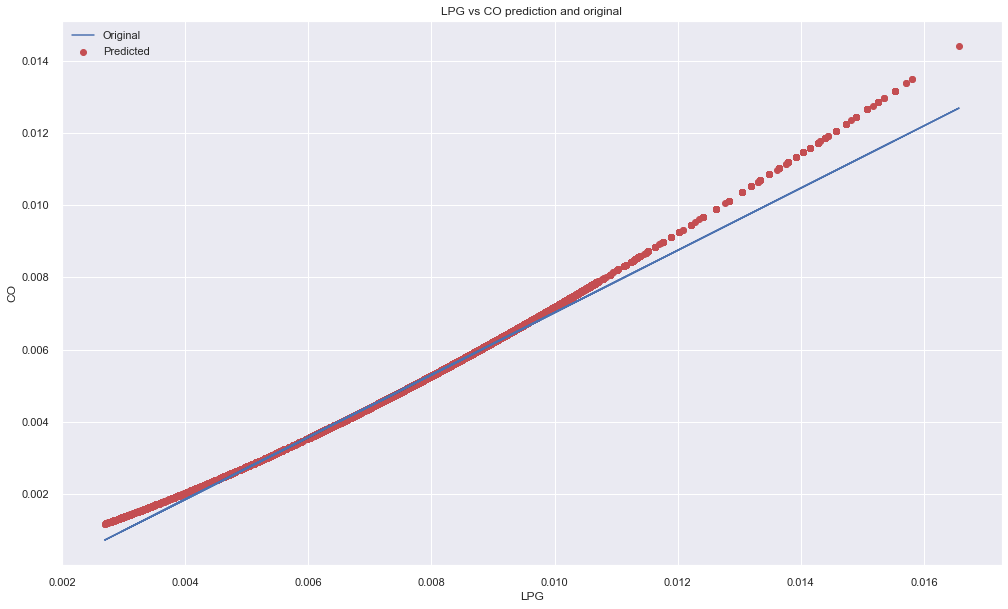
In above plot, the lines seems to be have fitted well for few data points but not for long because the relationship between LPG and CO might not be linear. So lets calculate error. There are many varieties of errors available and one of the popular is Mean Squared Error (MSE). It is very useful in regression because it takes all the points into consideration.

\[J{(\theta)} = \frac{1} {N} \sum_{i=1}^N (h_\theta (x^{(i)}) - y^{(i)})^2\]

The Mean Squared Error (MSE) or Mean Squared Deviation (MSD) of an estimator measures the average of error squares i.e. the average squared difference between the estimated values and true value. It is lesser the better.

We often use R2 Score to evaluate model’s strength. However, R2 score gives the strength of relationship between dependent and independent variable. If this score is 0.70, then it means that our dependent variable can be explained by 70% of the time using independent variable. R2 Score can be calculated as:

\[\begin{align} R^2&=1-\frac{\text{sum squared regression (SSR)}}{\text{total sum of squares (SST)}},\\ &=1-\frac{\sum({y_i}-\hat{y_i})^2}{\sum(y_i-\bar{y})^2}. \end{align}\]

In R2 Score, best possible score is 1.0 and it can be negative too when model is worse. And a model with constant output or change in input does not have effect in output would get R@ of 0.

from sklearn.metrics import mean_squared_error,r2_score

mean_squared_error(pred,y), r2_score(pred,y)

(8.330991934252437e-09, 0.9946397976368186)

Our error is very little but it could be just because our dependent and independent variables are small.

Multi Linear Regression

Instead of one independent variable, we will use two LPG and smoke here. A general equation is:

\[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + ..... \beta_n x_n\]

Further readings:

• Multi Linear Regression

X = df[["lpg", "smoke"]].to_numpy().reshape(-1,2)
y = df["co"].to_numpy().reshape(-1,1)

model = LinearRegression()

model.fit(X, y)

pred = model.predict(X)

print(f"Y intercept: {model.intercept_}, Slope: {model.coef_}")

Y intercept: [0.00047538], Slope: [[-4.00163949  1.71950252]]

mean_squared_error(pred,y), r2_score(pred,y)

(2.5074233596342503e-11, 0.999983952868222)

Error is not that much different so how about training different models?

Voting Regression

Voting regression is simple yet highly effective regression method where we train different models and then take the average of all to take the prediction. This can be best when we have different options of models and we have to find best result.

Further readings:

• Voting Regressor

For the sake of simplicity, we will use the code from above page and try to find best model.

We will train 3 regressors, Gradient Boosting, Random Forest and Linear Regressor.

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import VotingRegressor

reg1 = GradientBoostingRegressor(random_state=1)
reg2 = RandomForestRegressor(random_state=1)
reg3 = LinearRegression()

reg1.fit(X, y)
reg2.fit(X, y)
reg3.fit(X, y)

ereg = VotingRegressor([("gb", reg1), ("rf", reg2), ("lr", reg3)])
ereg.fit(X, y)

xt = X[:]

pred1 = reg1.predict(xt)
pred2 = reg2.predict(xt)
pred3 = reg3.predict(xt)
pred4 = ereg.predict(xt)

Now lets compare the MSE among these 4 models.

mean_squared_error(pred1,y),mean_squared_error(pred2,y),mean_squared_error(pred3,y),mean_squared_error(pred4,y)

(1.1387523048537922e-10,
 4.0783765489272603e-13,
 2.5074233596342503e-11,
 1.5792661424532076e-11)

r2_score(pred1,y),r2_score(pred2,y),r2_score(pred3,y),r2_score(pred4,y)

(0.9999270873961168, 0.999999738991435, 0.999983952868222, 0.9999898911749608)

All the models seems to be having similar r2 score but MSE was small for Random Forest Regressor.

Neural Networks

Neural networks are the algorithms inside a Deep Learning part of Machine Learning where we will mimic the neural structure of human brain and do computation to find the outputs. There are lots of algorithms made from Neural Networks, and simplest of them is Perceptron. Neural Networks can be used as both regressor and classifier and they are powerful, have higher level of model and much powerful than Linear Regression and Decision trees.

Neural Networks have few major steps while fitting a best models and those include:

• Feed Forward: Sending input values into the model.
• Activation: Calculating the input value into current node and getting the output of a node via applying activation function.
• Error Calculation: Comparing true label data with predicted data and finding the cost using error function.
• Back Propagation: Passing the error values towards input layers from output layer for weight update.
• Weight Update: The weights in neural networks are similar to the intercept and slope in linear regression model and they are the one what will try to find the as much as possible correct predictions. We have different weight update rules and popular of them is Gradient Descent.

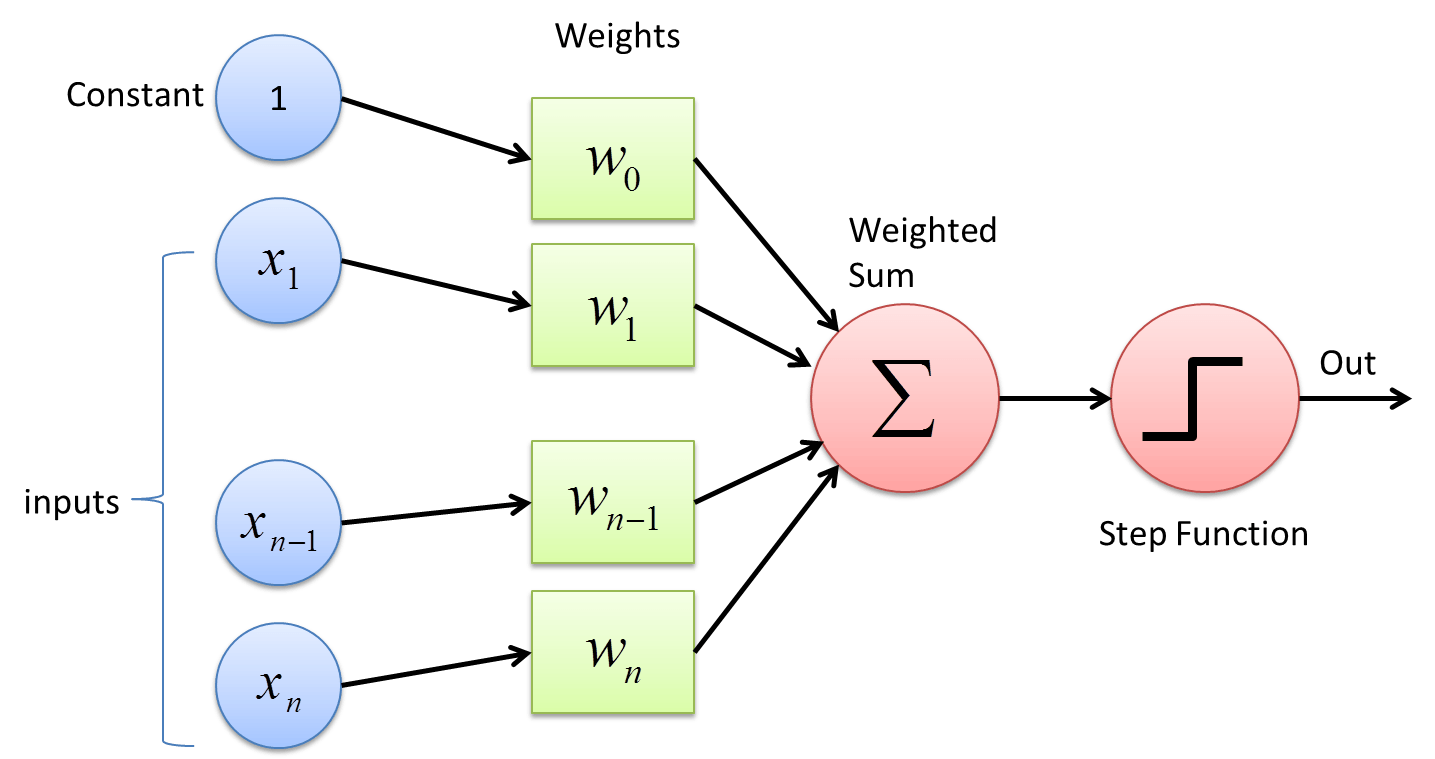Referenced from deepai.org.

Training a Multi Layer Neural Network

For simplicity, we will use keras. Keras is a high level deep learning framework built above the tensorflow.

!pip install keras

Requirement already satisfied: keras in c:\programdata\anaconda3\lib\site-packages (2.6.0)

from keras.models import Sequential
from keras.layers import Dense

s=X.shape[-1]

model = Sequential()
model.add(Dense(input_shape=(None,s),units=1))
model.add(Dense(units=1))

model.summary()

Model: "sequential_8"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_20 (Dense)             (None, None, 1)           3         
_________________________________________________________________
dense_21 (Dense)             (None, None, 1)           2         
=================================================================
Total params: 5
Trainable params: 5
Non-trainable params: 0
_________________________________________________________________

In above code, we have created a sequential model and it have 2 layers. First layer takes inputs and has 2 neurons and second layer also has 1 neuron and it is also a output layer. The parameters indicates how many parameters are there. For two inputs, there are two weight value and for one neuron there is one bias value. Thus we have 5 parameters.

Next we compile our model by passing optimizers and loss value. Optimizers are used to update the weights and parameters whereas loss is used to compute the error of prediction.

Below, we are taking Stochastic Gradient Descent as optimizer and Mean Squared Error as loss function. Then train a model for 5 epochs. We have also split our data by 0.2 and 0.8 part goes for training.

Above model is simply a linear model and it uses linear activation function.

model.compile(optimizer="sgd", loss="mse")
history = model.fit(X.reshape(-1,1,2),y, epochs=5, validation_split=0.2)

Epoch 1/5
10130/10130 [==============================] - 19s 2ms/step - loss: 4.3237e-05 - val_loss: 3.9576e-05
Epoch 2/5
10130/10130 [==============================] - 18s 2ms/step - loss: 4.1575e-05 - val_loss: 3.8815e-05
Epoch 3/5
10130/10130 [==============================] - 19s 2ms/step - loss: 4.0629e-05 - val_loss: 3.7956e-05
Epoch 4/5
10130/10130 [==============================] - 19s 2ms/step - loss: 3.9705e-05 - val_loss: 3.7445e-05
Epoch 5/5
10130/10130 [==============================] - 19s 2ms/step - loss: 3.8818e-05 - val_loss: 3.6460e-05

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()

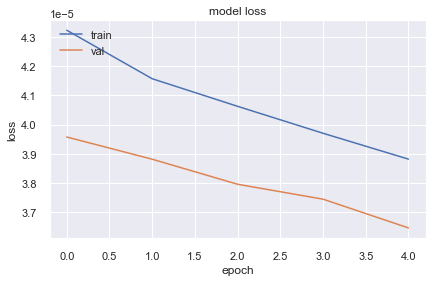
It seems loss is decreasing but not much faster. Lets create a new model with more complex architecture by adding more neuron and layers.

s=X.shape[-1]

model = Sequential()
model.add(Dense(input_shape=(None,s),units=2))
model.add(Dense(units=2))
model.add(Dense(units=1))

model.summary()

Model: "sequential_9"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_22 (Dense)             (None, None, 2)           6         
_________________________________________________________________
dense_23 (Dense)             (None, None, 2)           6         
_________________________________________________________________
dense_24 (Dense)             (None, None, 1)           3         
=================================================================
Total params: 15
Trainable params: 15
Non-trainable params: 0
_________________________________________________________________

model.compile(optimizer="sgd", loss="mse")
history = model.fit(X.reshape(-1,1,2),y, epochs=5, validation_split=0.2)

Epoch 1/5
10130/10130 [==============================] - 23s 2ms/step - loss: 1.7816e-05 - val_loss: 1.6430e-05
Epoch 2/5
10130/10130 [==============================] - 21s 2ms/step - loss: 1.7252e-05 - val_loss: 1.6075e-05
Epoch 3/5
10130/10130 [==============================] - 22s 2ms/step - loss: 1.6944e-05 - val_loss: 1.5883e-05
Epoch 4/5
10130/10130 [==============================] - 22s 2ms/step - loss: 1.6644e-05 - val_loss: 1.5597e-05
Epoch 5/5
10130/10130 [==============================] - 22s 2ms/step - loss: 1.6352e-05 - val_loss: 1.5316e-05

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()

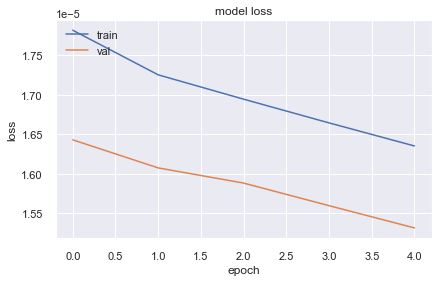
The loss is not decreasing as previous architecture lets try by changing activation function.

s=X.shape[-1]

model = Sequential()
model.add(Dense(input_shape=(None,s),units=2, activation="sigmoid"))
model.add(Dense(units=2, activation="sigmoid"))
model.add(Dense(units=1))

model.summary()

Model: "sequential_10"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_25 (Dense)             (None, None, 2)           6         
_________________________________________________________________
dense_26 (Dense)             (None, None, 2)           6         
_________________________________________________________________
dense_27 (Dense)             (None, None, 1)           3         
=================================================================
Total params: 15
Trainable params: 15
Non-trainable params: 0
_________________________________________________________________

model.compile(optimizer="sgd", loss="mse")
history = model.fit(X.reshape(-1,1,2),y, epochs=5, validation_split=0.2)

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()

Epoch 1/5
10130/10130 [==============================] - 22s 2ms/step - loss: 3.3142e-06 - val_loss: 1.8724e-06
Epoch 2/5
10130/10130 [==============================] - 22s 2ms/step - loss: 2.0107e-06 - val_loss: 1.9007e-06
Epoch 3/5
10130/10130 [==============================] - 22s 2ms/step - loss: 2.0104e-06 - val_loss: 1.8663e-06
Epoch 4/5
10130/10130 [==============================] - 22s 2ms/step - loss: 2.0102e-06 - val_loss: 1.8606e-06
Epoch 5/5
10130/10130 [==============================] - 22s 2ms/step - loss: 2.0100e-06 - val_loss: 1.8768e-06

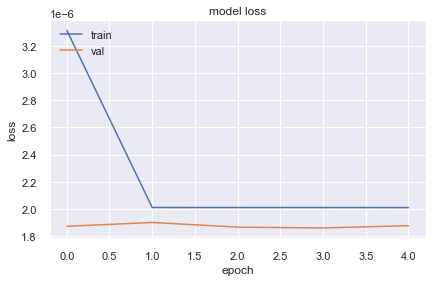
It does not look like loss is decreasing well after the first epoch and this might be because of having less data or bad model. So lets take few more columns and train a model.

cols = ["co", "humidity", "smoke", "temp"]

X = df[["lpg", "smoke", "temp", "humidity"]].to_numpy().reshape(-1,4)
y = df["co"].to_numpy().reshape(-1,1)

s=X.shape[-1]

model = Sequential()
model.add(Dense(input_shape=(None,s),units=2))
model.add(Dense(units=1))
model.add(Dense(units=1))

model.summary()

model.compile(optimizer="rmsprop", loss="mse")
history = model.fit(X.reshape(-1,1,s),y, epochs=5, validation_split=0.2)

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()

Model: "sequential_11"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_28 (Dense)             (None, None, 2)           10        
_________________________________________________________________
dense_29 (Dense)             (None, None, 1)           3         
_________________________________________________________________
dense_30 (Dense)             (None, None, 1)           2         
=================================================================
Total params: 15
Trainable params: 15
Non-trainable params: 0
_________________________________________________________________
Epoch 1/5
10130/10130 [==============================] - 22s 2ms/step - loss: 335.0356 - val_loss: 8.8038e-07
Epoch 2/5
10130/10130 [==============================] - 21s 2ms/step - loss: 1.3741e-06 - val_loss: 9.8763e-07
Epoch 3/5
10130/10130 [==============================] - 21s 2ms/step - loss: 1.3330e-06 - val_loss: 5.1773e-07
Epoch 4/5
10130/10130 [==============================] - 21s 2ms/step - loss: 1.3133e-06 - val_loss: 9.4256e-07
Epoch 5/5
10130/10130 [==============================] - 21s 2ms/step - loss: 1.3028e-06 - val_loss: 1.1142e-06

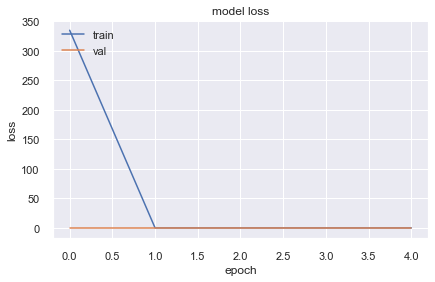
Conclusion

Neural Networks are very powerful algorithms and they work efficiently when used with huge chunk of data and right set of optimizer, loss function and architecture but not all data can be trained with Neural Networks. There are several reasons for that:

• Data could be very little to be trained with neural networks.
• Data could be not properly transformed. Which means that most of the model works when having dataset’s range small and similar.
• We might be trying to get best result by using wrong concepts like using illogical sets of activation function, optimizers, sample size and so on.

Conclusion from Regression

• Having a good model depends on the data, model architecture and cost function also.
• One have to do cross validation in order to get a better model and there is not a golden rule to get a best model.
• We we have some sort of linear relationship between train data and label then we should choose linear regression.
• If we have lot of ordinal, or categorical data, we should choose decision trees.
• If we have messy data and feature engineering is not our thing, then we should choose neural networks. But neural Nets does not guarantee that it will provide best model.

Classification

While regression was about to find a value, classification is about pushing or pulling data into one of several given classes. Regression is sensitive than the classification because regression has to map value with individual output while classification can give us some range. Just like regression, we many ways of doing classification and we should have the ability to choose the best algorithm according to the need and the quality of the data. Some of popular are:

• Logistic Regression
• Decision Trees
• Support Vector Machine
• Neural Networks

Logistic Regression

Logistic Regression is not a Regression algorithm as the name implies but it is a very powerful classifier. Mostly, we use Logistic Regression for binary classification but it works well with multiple labels too. The logistic name comes from the logistic function which can be defined as:

\[\sigma(x) = \frac{1}{1+e^{-x}}\]

A logistic regression can be defined as:

\[log\left( \frac{p(x)}{1-p(x)} \right)\]

But there are other variants of logistic regression that is used for multi label classification and for our case, we have to use Multi Label classification because we have 3 labels for 3 different devices. First we will create column where we will store ordinal values (0,1,2) from our string type of device. Then we will train a logistic regression model.

Gradient Descent is used to optimize the parameters in logistic regression.

Lets import necessary tools, we will split our data into train and test sets. We also have to scale all our data into same format and finally we will test our accuracy whether the predicted class is equal to the true class or not. And we will also use confusion matrix to find out how much of our data has been mislabeled.

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import plot_confusion_matrix

Make device column’s value as 0,12.

d={"00:0f:00:70:91:0a":0, 
   "1c:bf:ce:15:ec:4d":1,
   "b8:27:eb:bf:9d:51":2}
df["y"] = df.device.apply(lambda x: d[x])

Pick feature columns and train label from dataframe and scale it. Then we will split the data by 80/20 for train/test sets.

xcols = ["co", "humidity", "light", "lpg", "motion", "smoke", "temp"]
ycols = ["y"]

scaler = StandardScaler()

inp_df = scaler.fit_transform(X)
X = df[xcols]
y = df[ycols]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Now create a object of LogisticRegression and train a model.

clf = LogisticRegression()
clf.fit(X_train, y_train)

LogisticRegression()

Predict the labels for test data.

pred = clf.predict(X_test)

print(f"Accuracy: {accuracy_score(pred, y_test)}")

Accuracy: 0.9979021928254994

It seems that we scored 99.7% accuracy but this is abnormal case because this rarely happens in the real-world ML applications. However, we will still try to find best model than this one. We will do this by grid search. Grid search is a concept where we train multiple models wit different parameter and regularizations then find the model with accuracy from them.

from sklearn.model_selection import GridSearchCV

parameters_lr = [{'penalty':['l1','l2'],'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]}]
grid_search_lr = GridSearchCV(estimator = clf,
                           param_grid = parameters_lr,
                           scoring = 'accuracy',
                           cv = 10,
                           n_jobs = -1)
grid_search_lr.fit(X_train, y_train)
best_accuracy_lr = grid_search_lr.best_score_
best_paramaeter_lr = grid_search_lr.best_params_  
print("Best Accuracy of Logistic Regression: {:.2f} %".format(best_accuracy_lr.mean()*100))
print("Best Parameter of Logistic Regression:", best_paramaeter_lr)
print(f"Test Accuracy: {accuracy_score(pred, grid_search_lr.predict(X_test))}")

Best Accuracy of Logistic Regression: 99.91 %
Best Parameter of Logistic Regression: {'C': 0.001, 'penalty': 'l2'}
Test Accuracy: 0.9981983538383701

Confusion Matrix

plot_confusion_matrix(grid_search_lr,X_test,y_test)

<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x1e3e0d03f40>

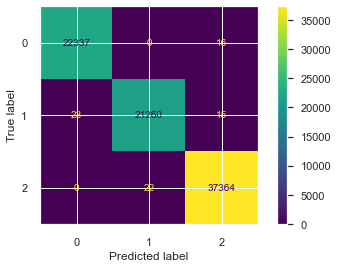
In above plot, we can see that there are only few misclassification. So our accuracy was high. But for the model to be good, one have to calculate classifier’s f1 score. The formula of F1 Score is: \(F1 = 2 \frac{precision * recall}{precision + recall}\)

Where,

• Precision: $P = \frac{T_p}{T_p+F_p}$
• Recall: $R = \frac{T_p}{T_p + F_n}$

Readings:

• Precision and Recall

from sklearn.metrics import f1_score

f1_score(y_test, pred, average='macro')

0.9978626630082132

Which seems that our model is great.

Decision Trees

Decision trees are nothing but a if else but they are pretty powerful classifier if we well scaled data. Lets train a decision tree and see its performance.

from sklearn.tree import DecisionTreeClassifier

clf = DecisionTreeClassifier()

# Train Decision Tree Classifer
clf = clf.fit(X_train,y_train)

#Predict the response for test dataset
y_pred = clf.predict(X_test)
print(f"Accuracy: ",accuracy_score(y_test,y_pred))

Accuracy:  0.999987659957797

from sklearn.metrics import f1_score

f1_score(y_test, y_pred, average='macro')

0.9999847184014105

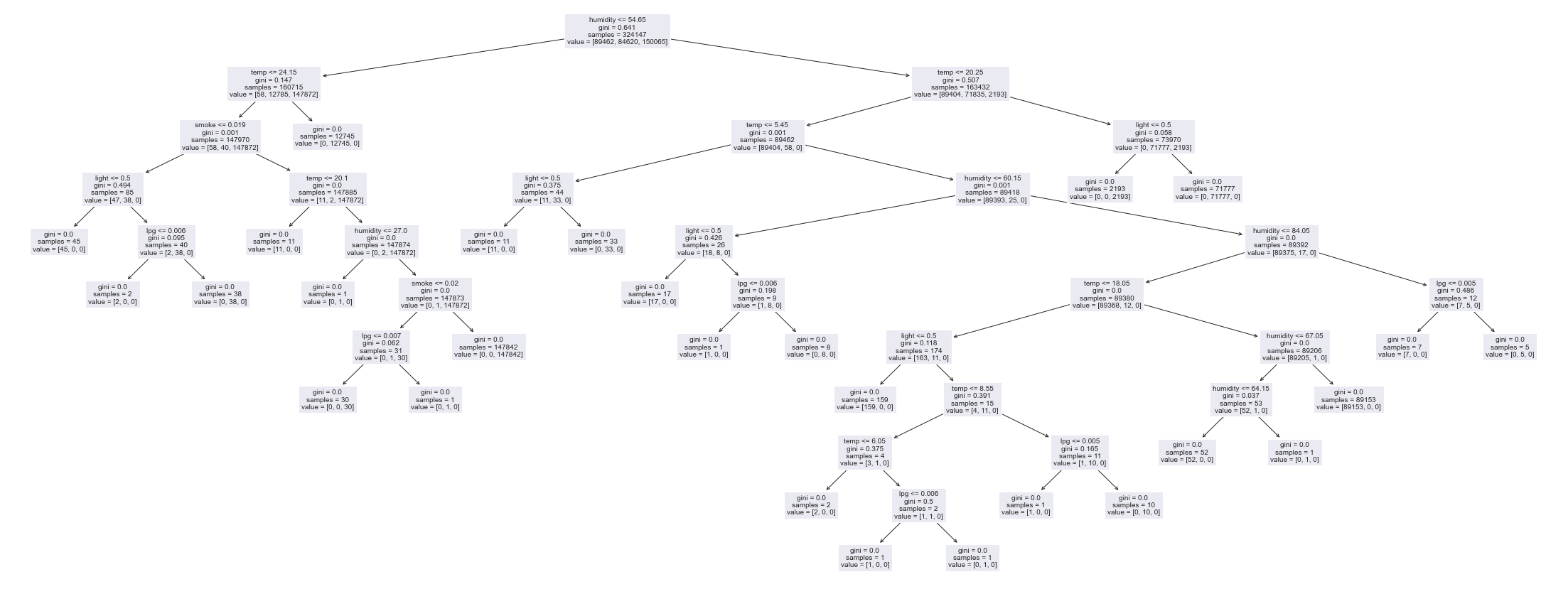
The accuracy is even better than that of Logistic Regression but this is just a simple decision tree. Lets visualize the trained tree.

from sklearn import tree

plt.figure(figsize=(35,15))
tree.plot_tree(clf, feature_names=xcols, fontsize=10, )
plt.show()

Neural Network

Classification in neural network is much robust than regression and with the availability of different algorithms and optimizers, one could do this with ease. But first we have to convert our y label into one hot encoded vector. Instead of a default linear activation function, we will use softmax. It is gives us the probability of being a input from all the classes and we pick one with highest value.

\[softmax(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{N}e^{x_j}}\]

And for a loss function, we will use categorical crossentropy.

\[loss = - \frac{1}{N} \sum_{i=0}^{N-1}y_I. log(\hat{y}_i) + (1-y_i) . log(1-\hat{y}_i)\]

from keras.models import Sequential
from keras.layers import Dense
from keras.utils.np_utils import to_categorical

y_cat = to_categorical(y, num_classes=3)

In above, we have converted our y label into one hot encoded vector which contains 3 categories.

s=X.shape[-1]

model = Sequential()
model.add(Dense(input_shape=(None,s),units=1))
model.add(Dense(units=3, activation="softmax"))

model.summary()

Model: "sequential_12"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_31 (Dense)             (None, None, 1)           8         
_________________________________________________________________
dense_32 (Dense)             (None, None, 3)           6         
=================================================================
Total params: 14
Trainable params: 14
Non-trainable params: 0
_________________________________________________________________

model.compile(optimizer="sgd",loss="categorical_crossentropy", metrics=["acc"])
history = model.fit(X.to_numpy().astype('float32').reshape(-1,1,s), 
                    y_cat.reshape(-1, 1, 3), 
                    epochs=10, validation_split=0.2)

Epoch 1/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.5513 - acc: 0.7361 - val_loss: 0.4639 - val_acc: 0.8126
Epoch 2/10
10130/10130 [==============================] - 19s 2ms/step - loss: 0.5213 - acc: 0.7562 - val_loss: 1.3306 - val_acc: 0.4629
Epoch 3/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.4799 - acc: 0.8367 - val_loss: 0.5317 - val_acc: 0.7061
Epoch 4/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.3789 - acc: 0.8906 - val_loss: 0.2480 - val_acc: 0.9916
Epoch 5/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.2927 - acc: 0.9238 - val_loss: 0.1168 - val_acc: 0.9945
Epoch 6/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.2451 - acc: 0.9417 - val_loss: 0.0849 - val_acc: 0.9947
Epoch 7/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.2162 - acc: 0.9509 - val_loss: 0.0621 - val_acc: 0.9947
Epoch 8/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.2034 - acc: 0.9559 - val_loss: 0.0693 - val_acc: 0.9947
Epoch 9/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.1931 - acc: 0.9598 - val_loss: 0.0667 - val_acc: 0.9947
Epoch 10/10
10130/10130 [==============================] - 20s 2ms/step - loss: 0.1894 - acc: 0.9613 - val_loss: 0.0629 - val_acc: 0.9947

As looking over above results, our model is not training once it reached 96% train accuracy. Can we improve this by adding more layers?

s=X.shape[-1]

model = Sequential()
model.add(Dense(input_shape=(None,s),units=5))
model.add(Dense(units=3))
model.add(Dense(units=3, activation="softmax"))

model.summary()

model.compile(optimizer="sgd",loss="categorical_crossentropy", metrics=["acc"])
history = model.fit(X.to_numpy().astype('float32').reshape(-1,1,s), 
                    y_cat.reshape(-1, 1, 3), 
                    epochs=10, validation_split=0.2)

Model: "sequential_13"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_33 (Dense)             (None, None, 5)           40        
_________________________________________________________________
dense_34 (Dense)             (None, None, 3)           18        
_________________________________________________________________
dense_35 (Dense)             (None, None, 3)           12        
=================================================================
Total params: 70
Trainable params: 70
Non-trainable params: 0
_________________________________________________________________
Epoch 1/10
10130/10130 [==============================] - 24s 2ms/step - loss: 0.3519 - acc: 0.8768 - val_loss: 0.0417 - val_acc: 0.9994
Epoch 2/10
10130/10130 [==============================] - 24s 2ms/step - loss: 0.1237 - acc: 0.9705 - val_loss: 0.0833 - val_acc: 0.9991
Epoch 3/10
10130/10130 [==============================] - 23s 2ms/step - loss: 0.0850 - acc: 0.9775 - val_loss: 0.0168 - val_acc: 0.9994
Epoch 4/10
10130/10130 [==============================] - 23s 2ms/step - loss: 0.0759 - acc: 0.9790 - val_loss: 0.0330 - val_acc: 0.9993
Epoch 5/10
10130/10130 [==============================] - 23s 2ms/step - loss: 0.0721 - acc: 0.9797 - val_loss: 0.0196 - val_acc: 0.9945
Epoch 6/10
10130/10130 [==============================] - 23s 2ms/step - loss: 0.0692 - acc: 0.9810 - val_loss: 0.0141 - val_acc: 0.9994
Epoch 7/10
10130/10130 [==============================] - 23s 2ms/step - loss: 0.0629 - acc: 0.9818 - val_loss: 0.0198 - val_acc: 0.9946
Epoch 8/10
10130/10130 [==============================] - 23s 2ms/step - loss: 0.0644 - acc: 0.9820 - val_loss: 0.0941 - val_acc: 0.9993
Epoch 9/10
10130/10130 [==============================] - 23s 2ms/step - loss: 0.0563 - acc: 0.9834 - val_loss: 0.0162 - val_acc: 0.9993
Epoch 10/10
10130/10130 [==============================] - 23s 2ms/step - loss: 0.0573 - acc: 0.9844 - val_loss: 0.0366 - val_acc: 0.9993

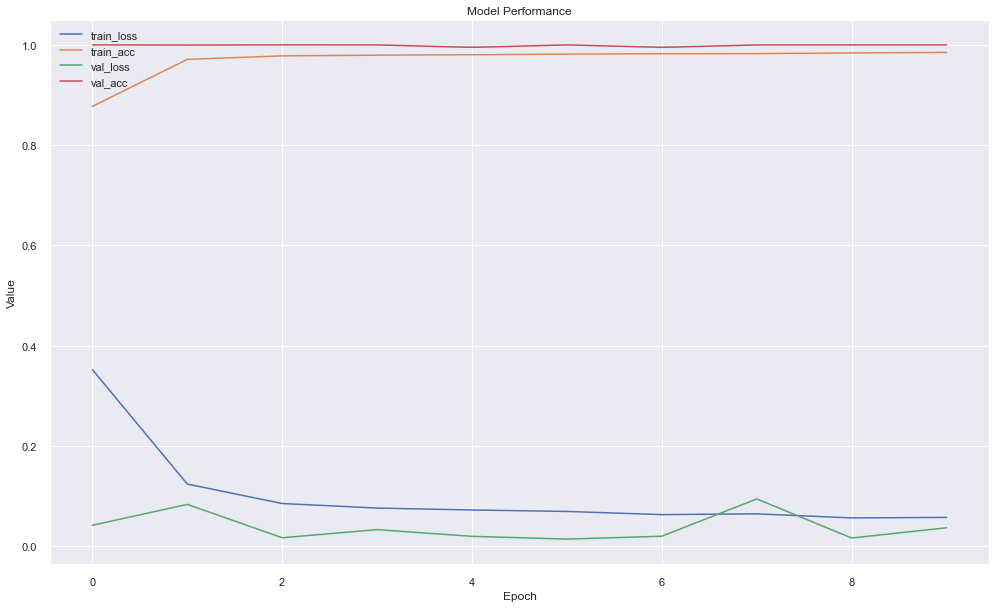
Now the model’s validation accuracy seems to be increased little bit (from 99.47% to 99.94%). Also training accuracy has increased little bit and loose is also on the verge of decreasing. If we train for a little bit, we might get little bit far but that will not always be a case, as model might get overfitted.

plt.figure(figsize=(15,10))
plt.plot(history.history['loss'])
plt.plot(history.history['acc'])
plt.plot(history.history['val_loss'])
plt.plot(history.history['val_acc'])
plt.title('Model Performance')
plt.ylabel('Value')
plt.xlabel('Epoch')
plt.legend(['train_loss', 'train_acc', 'val_loss', 'val_acc'], loc='upper left')
plt.show()

Conclusion from Classification

• Decision trees are powerful algorithms and they provide great result if we have our data preprocessed well and done feature engineering.
• Logistic regression are best when we have binary label and we are simply trying to push/pull data into one of two classes. But it does work with multi label too.
• Neural networks are best when we have lots of data and performing feature engineering is a time consuming task. But we have to experiment with different model architectures, loss, optimizer and learning rates.