Quassarian Viper

Quassarian Viper

Pile of Quarks as Homo Sapiens.

Python for Stock Market Analysis: Working with Moving Averages

13 minute read

Introduction

This blog is a first part of our series Python for Stock Market Analysis.

Disclaimer: This blog is for educational purpose only and we do not recommend taking the knowledge gained from this blog to implement in real financial exercises.

This blog tries to implement preliminary metrics that are used in the stock market analysis. The dataset we will be using is available via yahoofinance.

For interactive version of this blog, please visit this link.

Preliminary Actions

Install Libraries

Please install:

  • YahooFinance as pip install yfinance for downloading data of stock’s history.
  • Pandas as pip install pandas for data analysis.
  • Plotly as pip install plotly for interactive visualizations.
  • Cufflinks as pip install cufflinks for using interactive plots in pandas DataFrame.

You might need to install pip install -U kaleido if you need to save plots as png image.

If you are new into plotly, then we have an awesome blog about it where we have done plots based on COVID 19 dataset.

!pip install yfinance

Requirement already satisfied: yfinance in c:\programdata\anaconda3\lib\site-packages (0.1.63)
Requirement already satisfied: numpy>=1.15 in c:\users\dell\appdata\roaming\python\python38\site-packages (from yfinance) (1.19.5)
Requirement already satisfied: requests>=2.20 in c:\users\dell\appdata\roaming\python\python38\site-packages (from yfinance) (2.26.0)
Requirement already satisfied: multitasking>=0.0.7 in c:\programdata\anaconda3\lib\site-packages (from yfinance) (0.0.9)
Requirement already satisfied: pandas>=0.24 in c:\programdata\anaconda3\lib\site-packages (from yfinance) (1.2.4)
Requirement already satisfied: lxml>=4.5.1 in c:\programdata\anaconda3\lib\site-packages (from yfinance) (4.6.3)
Requirement already satisfied: pytz>=2017.3 in c:\programdata\anaconda3\lib\site-packages (from pandas>=0.24->yfinance) (2021.1)
Requirement already satisfied: python-dateutil>=2.7.3 in c:\programdata\anaconda3\lib\site-packages (from pandas>=0.24->yfinance) (2.8.1)
Requirement already satisfied: six>=1.5 in c:\programdata\anaconda3\lib\site-packages (from python-dateutil>=2.7.3->pandas>=0.24->yfinance) (1.15.0)
Requirement already satisfied: charset-normalizer~=2.0.0 in c:\users\dell\appdata\roaming\python\python38\site-packages (from requests>=2.20->yfinance) (2.0.7)
Requirement already satisfied: urllib3<1.27,>=1.21.1 in c:\programdata\anaconda3\lib\site-packages (from requests>=2.20->yfinance) (1.26.4)
Requirement already satisfied: certifi>=2017.4.17 in c:\programdata\anaconda3\lib\site-packages (from requests>=2.20->yfinance) (2020.12.5)
Requirement already satisfied: idna<4,>=2.5 in c:\programdata\anaconda3\lib\site-packages (from requests>=2.20->yfinance) (2.10)

Import Required Libraries

import pandas as pd
import plotly.express as px
import cufflinks
import plotly.io as pio 
import yfinance as yf
cufflinks.go_offline()
cufflinks.set_config_file(world_readable=True, theme='pearl')
pio.renderers.default = "notebook" # should change by looking into pio.renderers

pd.options.display.max_columns = None

Download Stock Data of Apple

By default, we are allowed to download data from 1900-01-01

symbols = ["AAPL"]

df = yf.download(tickers=symbols)
df.head()

[*********************100%***********************]  1 of 1 completed
Open High Low Close Adj Close Volume
Date
1980-12-12 0.128348 0.128906 0.128348 0.128348 0.100326 469033600
1980-12-15 0.122210 0.122210 0.121652 0.121652 0.095092 175884800
1980-12-16 0.113281 0.113281 0.112723 0.112723 0.088112 105728000
1980-12-17 0.115513 0.116071 0.115513 0.115513 0.090293 86441600
1980-12-18 0.118862 0.119420 0.118862 0.118862 0.092911 73449600

It seems that data is only available from 1980-12-12. The column names in the above fields are:

  • Open: It is the price of the stock at the start of the day of that date.
  • Close: It is the price of the stock at the end of that date.
  • High: It is the highest price of the stock on that date.
  • Low: It is the lowest price of the stock on that date.
  • Volume: It is the number of shares traded on that date.

Perform EDA

EDA or Exploratory Data Analysis is the first step in any Data Analysis and lets do that in our Stock Data too. We have blogs about doing EDA, Statistical and Inferential Analysis please check them out for more about EDAs.

Checking for Null Value

# convert column names into lowercase
df.columns = [c.lower() for c in df.columns]

ndf = pd.DataFrame()
for c in df.columns:
    nc = df[c].isna().sum()
    tr = len(df[c])
    rate = nc/tr
    ndf = ndf.append({"col_name":c,"total_rows": tr, 
                "null_rows": nc,
                "rate": rate},ignore_index=True)
ndf
col_name null_rows rate total_rows
0 open 0.0 0.0 10390.0
1 high 0.0 0.0 10390.0
2 low 0.0 0.0 10390.0
3 close 0.0 0.0 10390.0
4 adj_close 0.0 0.0 10390.0
5 volume 0.0 0.0 10390.0

It seems that we do not have any null rows present on the data.

View the Distribution

It gives us the frequency of value’s some range. It is simply a histogram.

fig = df.iplot(kind="hist",subplots=True, title="Distribution of All Variables", asFigure=True)
fig.write_image("stock_analysis/dist.png")
fig.show()

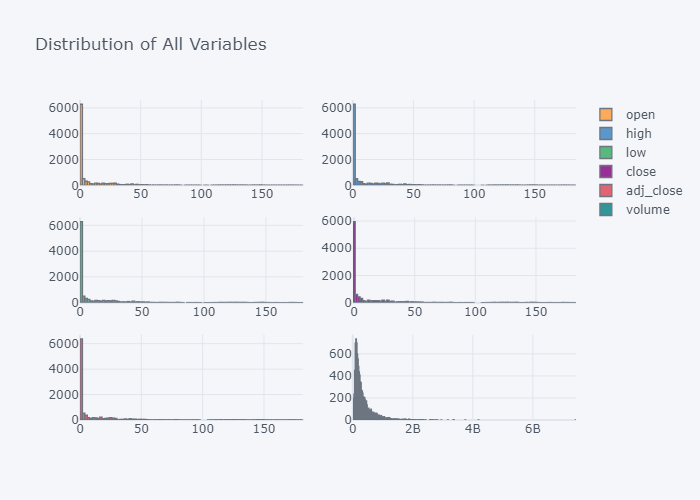
It seems that all values of the columns are left tailed.

View the Box Plot

Box Plot gives the clear picture of our descriptive nature of the data.

fig = df.iplot(kind="box",subplots=True, title="Box of All Variables", asFigure=True)
fig.write_image("stock_analysis/box.png")
fig.show()

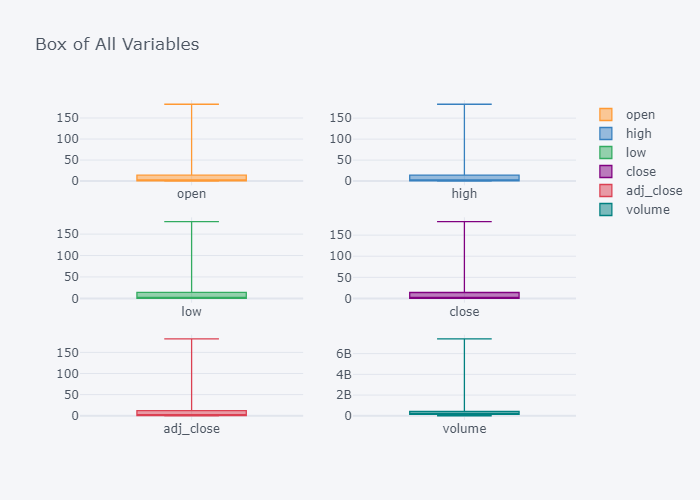
It seems that we have too many outliers but it does not matter right now.

Summary of our data

df.describe()
open high low close adj_close volume
count 10390.000000 10390.000000 10390.000000 10390.000000 10390.000000 1.039000e+04
mean 13.689530 13.837209 13.542035 13.695320 13.077773 3.326112e+08
std 29.525352 29.857351 29.199483 29.542847 29.249790 3.394925e+08
min 0.049665 0.049665 0.049107 0.049107 0.038385 0.000000e+00
25% 0.281250 0.287946 0.273996 0.281250 0.234167 1.251712e+08
50% 0.466518 0.476004 0.459732 0.466518 0.385693 2.205952e+08
75% 14.034375 14.205357 13.918214 14.033482 12.025377 4.136293e+08
max 182.630005 182.940002 179.119995 182.009995 181.778397 7.421641e+09

Box Plot already gave us the summary of the data. We can see that the average volume is 3.326112e+08 but will it give a true picture about the volume’s flow over the course of the time? It won’t because there will be certain rise and falls of the values over the time. Lets try to visualize it as line plot.

fig=df.iplot(kind="line",subplots=True, title="Trend of All Variables", asFigure=True)
fig.write_image("stock_analysis/trend.png")
fig.show()

As we can see in the above plot that, the trend of the OHLC is in increasing order while Volume is not. The values of share increases/decreases but in overall, it seems to be increasing.

Moving Average

Moving average is a kind of average where we take the average of data within some time frame only. While looking at the time series data that have high volatility (e.g. standard deviation), the simple average DOES NOT give a clear picture of the mean or average value. One reason is that, in real world financial data, the amount/price does increase/decrease with some unexpected factors like COVID outbreak, or expected factors like Tesla’s new car. So to get the figure that will well represent the average amount, we will take the average over some time only. By doing so, we wont be caring much about the history that is too much old and does not affect much to our present.

Simple Moving Average (SMA)

Simple Moving Average is the simplest example of the Moving Average where we take the data from some time frame and divide it by number of data points. The size of the time frame is often known as the window of movement. It is an example of Technical Indicator (heuristic or pattern-based signals produced by the price or volume).

A formula to calculate Simple Moving Average is:

\[SMA = \frac{V_1 + V_2 + V_3 + ... + V_n}{n}\]

Where,

  • V is a value at period n
  • n is number of periods

Lets try to implement this concept in our data, we will take window size or n as 5.

tdf = df.copy()
smadf = tdf.rolling(window=5).mean()
smadf
open high low close adj_close volume
Date
1980-12-12 NaN NaN NaN NaN NaN NaN
1980-12-15 NaN NaN NaN NaN NaN NaN
1980-12-16 NaN NaN NaN NaN NaN NaN
1980-12-17 NaN NaN NaN NaN NaN NaN
1980-12-18 0.119643 0.119978 0.119420 0.119420 0.093347 182107520.0
... ... ... ... ... ... ...
2022-02-18 170.208002 171.663998 168.304001 170.080002 170.080002 72770540.0
2022-02-22 169.730002 171.085999 167.422000 169.168002 169.168002 73766000.0
2022-02-23 168.644000 169.725998 165.322000 166.624005 166.624005 78910580.0
2022-02-24 164.789999 167.628000 161.712000 164.662006 164.662006 94904600.0
2022-02-25 163.351999 166.269998 160.191998 163.856006 163.856006 99363080.0

10390 rows × 6 columns



for c in smadf.columns:
    tdf[f"sma_{c}"] = smadf[c]
tdf
open high low close adj_close volume sma_open sma_high sma_low sma_close sma_adj_close sma_volume
Date
1980-12-12 0.128348 0.128906 0.128348 0.128348 0.100326 469033600 NaN NaN NaN NaN NaN NaN
1980-12-15 0.122210 0.122210 0.121652 0.121652 0.095092 175884800 NaN NaN NaN NaN NaN NaN
1980-12-16 0.113281 0.113281 0.112723 0.112723 0.088112 105728000 NaN NaN NaN NaN NaN NaN
1980-12-17 0.115513 0.116071 0.115513 0.115513 0.090293 86441600 NaN NaN NaN NaN NaN NaN
1980-12-18 0.118862 0.119420 0.118862 0.118862 0.092911 73449600 0.119643 0.119978 0.119420 0.119420 0.093347 182107520.0
... ... ... ... ... ... ... ... ... ... ... ... ...
2022-02-18 169.820007 170.539993 166.190002 167.300003 167.300003 82614200 170.208002 171.663998 168.304001 170.080002 170.080002 72770540.0
2022-02-22 164.979996 166.690002 162.149994 164.320007 164.320007 91162800 169.730002 171.085999 167.422000 169.168002 169.168002 73766000.0
2022-02-23 165.539993 166.149994 159.750000 160.070007 160.070007 90009200 168.644000 169.725998 165.322000 166.624005 166.624005 78910580.0
2022-02-24 152.580002 162.850006 152.000000 162.740005 162.740005 141147500 164.789999 167.628000 161.712000 164.662006 164.662006 94904600.0
2022-02-25 163.839996 165.119995 160.869995 164.850006 164.850006 91881700 163.351999 166.269998 160.191998 163.856006 163.856006 99363080.0

10390 rows × 12 columns

Plotting SMA of All

smac = [c for c in tdf.columns if "sma" in c]
col = [c for c in tdf.columns if "sma" not in c]

for s,c in zip(smac,col):
    fig = tdf[[c, s]].iplot(kind="line", title=f"{s} vs {c}", xTitle="Date", asFigure=True)
    fig.write_image(f"stock_analysis/sma_{c}.png")
    fig.show()

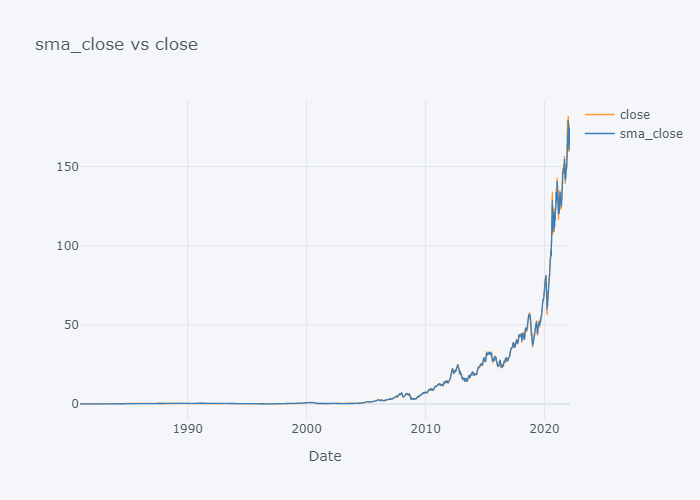
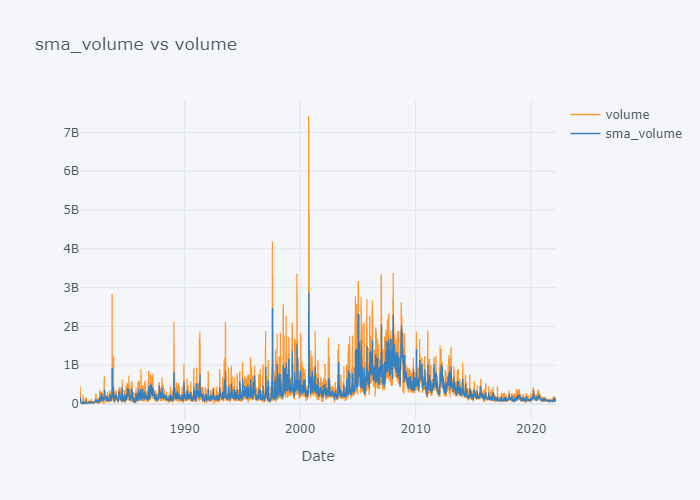
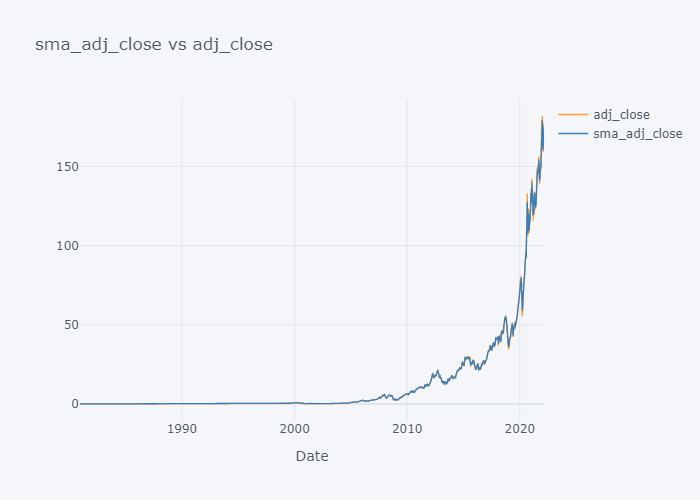
We can not see the much difference between WMA and SMA and it is because of the level (daily) of our data. Lets try to plot data of last 100 days only.

for s,c,w in zip(smac,col, wmac):
    fig=tdf[-100:][[c, s, w]].iplot(kind="line", title=f"{s} vs {c} vs {w}",  xTitle="Date", asFigure=True)
    fig.write_image(f"stock_analysis/sma_{c}2.png")
    fig.show()

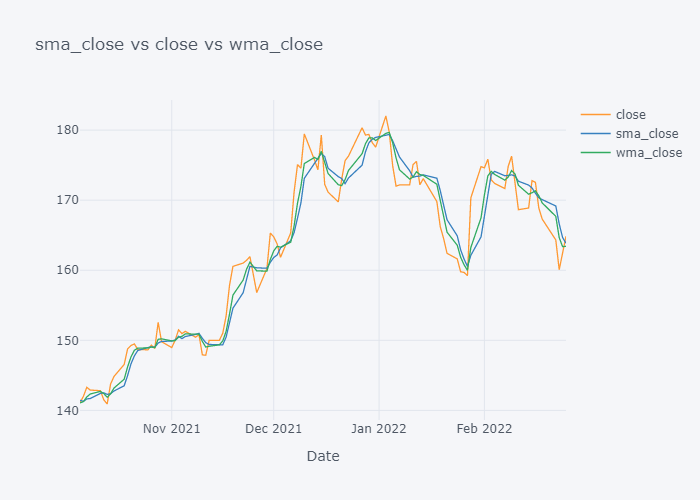
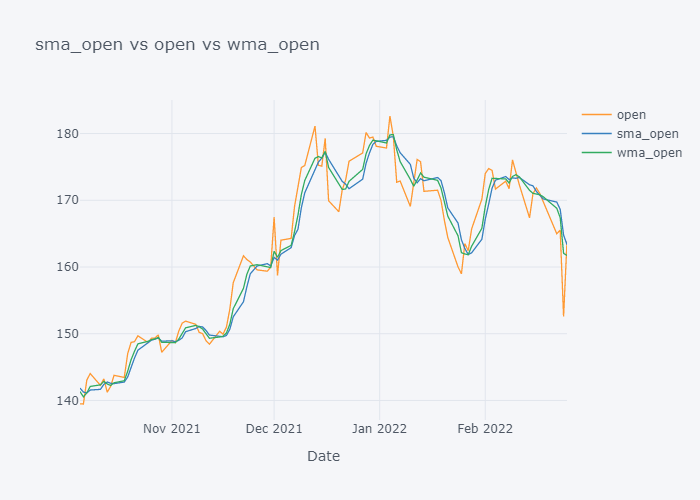
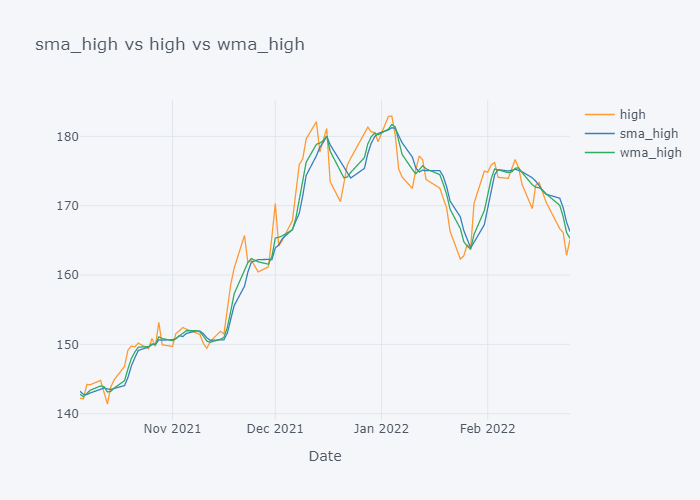
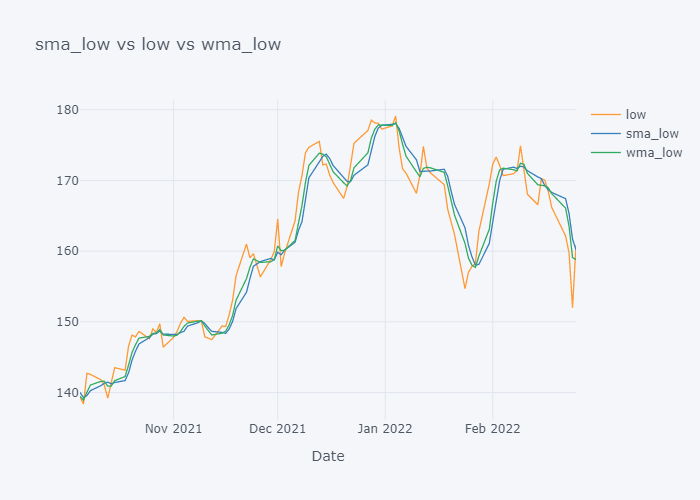
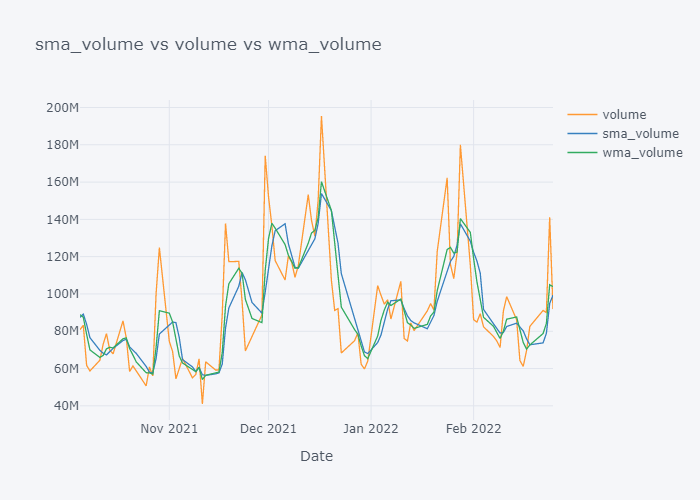
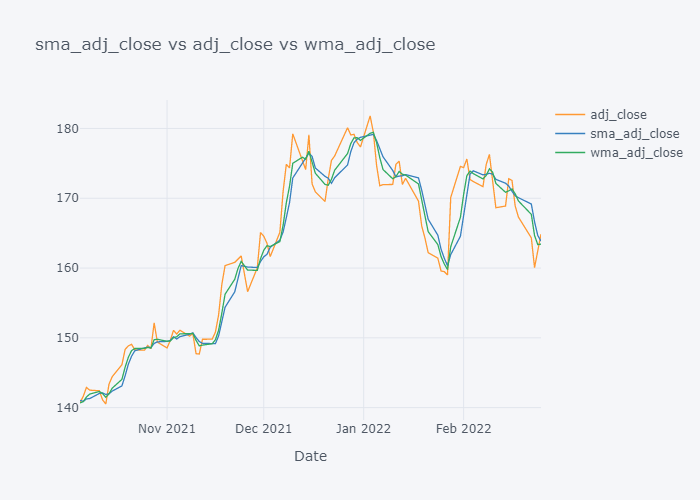
Now it is more clearer. Looking over the plot of open,

  • We can clearly see that the default value of the open have some spikes and huge downfalls.
  • But the value of SMA and WMA is not getting affected that much by those sudden rise/fall in the value because it contains the value from the past.
  • If we look over the November to December, the Open value is increasing rapidly but the SMA is increasing slowly because it knows that there were some small values in last 5 days. Similarly WMA is also increasing slowly. But we can see that WMA is always much nearer to the Open value because it is giving much importance to the latest value.
  • The sudden rise/fall in open is not the sign or price up/down in long run because one must always consider moving averages.

Exponential Moving Average (EMA)

It is similar to the WMA in the sense of giving weights to values but, instead of the linear weights, we will give exponential weights.

A general formula of EMA at time t is:

\[EMA_t = \left[V_t * \left(\frac{s}{1+d}\right)\right] + EMA_y * \left[1-\left(\frac{s}{1+d}\right)\right]\]

Where,

  • EMAt is EMA value at t
  • Vt is value at t
  • EMAy is EMA at t-1
  • s is smoothing parameter
  • d is number of ts

Purpose of using EMA is to give high weights to more recent values and shows more sensitivity to more recent data. This average is more responsive to the latest price changes than SMA.

We do not have to use this scary formula from the scratch because pandas gives us some ways to do it with little code. Please refer to Pandas documentation for more info about EWM.

\[y_0 = x_0 \\\ y_t = (1 - \alpha) y_{t-1} + \alpha x_t,\]

Where, alpha is either the value given by us or smoothing/(time periods+1). Smoothing is generally taken as 2 and time periods is taken as our requirement.

emadf=df.ewm(span=5, min_periods=5, adjust=True).mean()
emadf
open high low close adj_close volume
Date
1980-12-12 NaN NaN NaN NaN NaN NaN
1980-12-15 NaN NaN NaN NaN NaN NaN
1980-12-16 NaN NaN NaN NaN NaN NaN
1980-12-17 NaN NaN NaN NaN NaN NaN
1980-12-18 0.118153 0.118552 0.117994 0.117994 0.092232 1.239301e+08
... ... ... ... ... ... ...
2022-02-18 170.786802 171.961456 168.279383 169.672761 169.670227 7.574409e+07
2022-02-22 168.851200 170.204305 166.236253 167.888510 167.886821 8.088366e+07
2022-02-23 167.747464 168.852868 164.074169 165.282342 165.281216 8.392551e+07
2022-02-24 162.691644 166.851914 160.049446 164.434897 164.434146 1.029995e+08
2022-02-25 163.074428 166.274608 160.322962 164.573267 164.572766 9.929357e+07

10390 rows × 6 columns

for c in emadf.columns:
    tdf[f"ema_{c}"] = emadf[c]
tdf
open high low close adj_close volume sma_open sma_high sma_low sma_close sma_adj_close sma_volume wma_open wma_high wma_low wma_close wma_adj_close wma_volume ema_open ema_high ema_low ema_close ema_adj_close ema_volume
Date
1980-12-12 0.128348 0.128906 0.128348 0.128348 0.100326 469033600 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1980-12-15 0.122210 0.122210 0.121652 0.121652 0.095092 175884800 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1980-12-16 0.113281 0.113281 0.112723 0.112723 0.088112 105728000 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1980-12-17 0.115513 0.116071 0.115513 0.115513 0.090293 86441600 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1980-12-18 0.118862 0.119420 0.118862 0.118862 0.092911 73449600 0.119643 0.119978 0.119420 0.119420 0.093347 182107520.0 0.117932 0.118304 0.117746 0.117746 0.092038 1.234001e+08 0.118153 0.118552 0.117994 0.117994 0.092232 1.239301e+08
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2022-02-18 169.820007 170.539993 166.190002 167.300003 167.300003 82614200 170.208002 171.663998 168.304001 170.080002 170.080002 72770540.0 170.538670 171.722664 168.136002 169.608669 169.608669 7.264790e+07 170.786802 171.961456 168.279383 169.672761 169.670227 7.574409e+07
2022-02-22 164.979996 166.690002 162.149994 164.320007 164.320007 91162800 169.730002 171.085999 167.422000 169.168002 169.168002 73766000.0 168.796001 170.064666 166.084666 167.688671 167.688671 7.877865e+07 168.851200 170.204305 166.236253 167.888510 167.886821 8.088366e+07
2022-02-23 165.539993 166.149994 159.750000 160.070007 160.070007 90009200 168.644000 169.725998 165.322000 166.624005 166.624005 78910580.0 167.399332 168.419331 163.527333 164.656006 164.656006 8.419305e+07 167.747464 168.852868 164.074169 165.282342 165.281216 8.392551e+07
2022-02-24 152.580002 162.850006 152.000000 162.740005 162.740005 141147500 164.789999 167.628000 161.712000 164.662006 164.662006 94904600.0 162.044666 166.127334 159.086666 163.361339 163.361339 1.049387e+08 162.691644 166.851914 160.049446 164.434897 164.434146 1.029995e+08
2022-02-25 163.839996 165.119995 160.869995 164.850006 164.850006 91881700 163.351999 166.269998 160.191998 163.856006 163.856006 99363080.0 161.727998 165.291332 158.805998 163.424006 163.424006 1.039311e+08 163.074428 166.274608 160.322962 164.573267 164.572766 9.929357e+07

10390 rows × 24 columns

Plotting EMA of All

Instead viewing EMA of entire data, lets view it of last 100 days only.

smac = [c for c in tdf.columns if "sma" in c]
wmac = [c for c in tdf.columns if "wma" in c]
emac = [c for c in tdf.columns if "ema" in c]
col = [c for c in tdf.columns if "sma" not in c and "wma" not in c and "ema" not in c]

for s,c,w,e in zip(smac,col, wmac, emac):
    fig=tdf[-100:][[c, s, w, e]].iplot(kind="line", title=f"{s} vs {c} vs {w} vs {e}", xTitle="Date", asFigure=True)
    fig.write_image(f"stock_analysis/ema_{c}.png")
    fig.show()

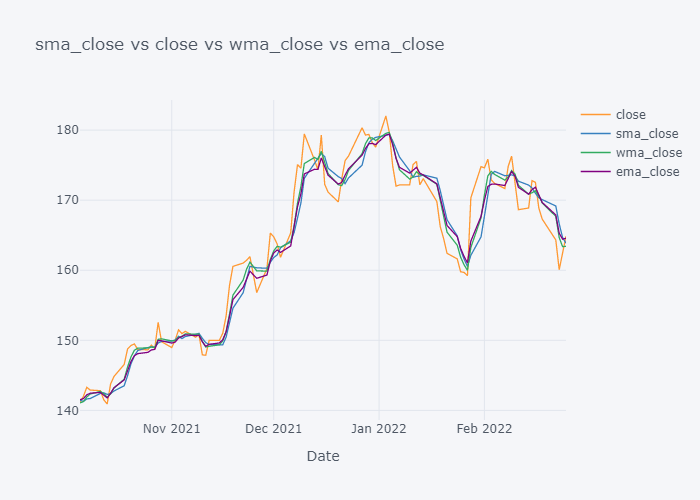
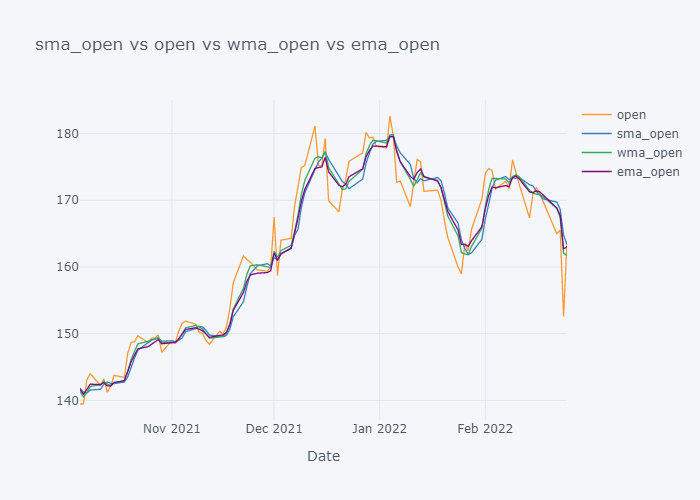
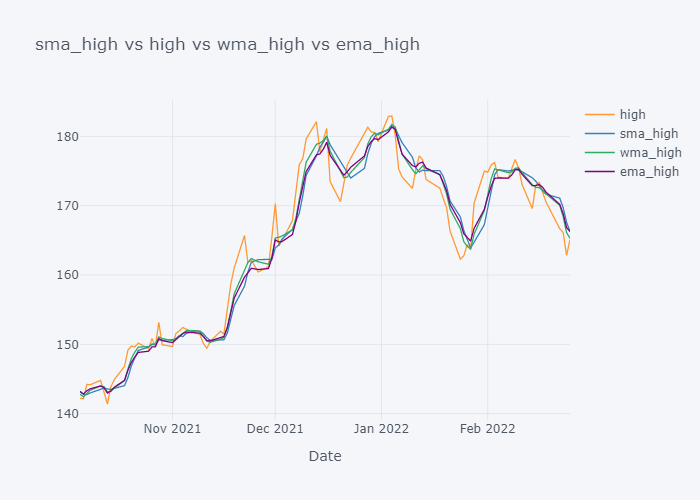
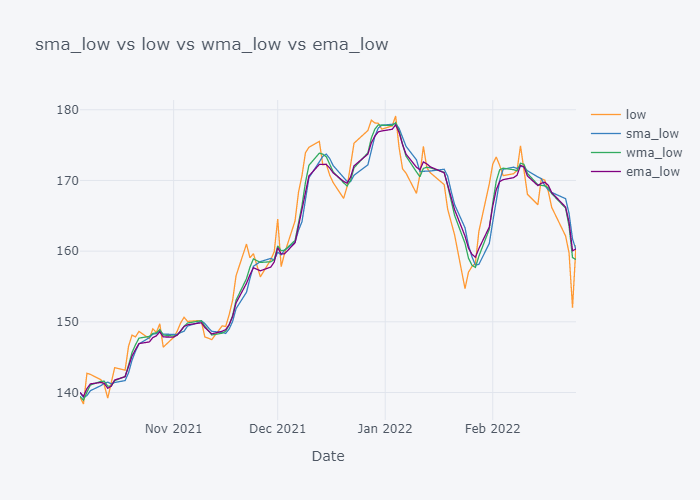
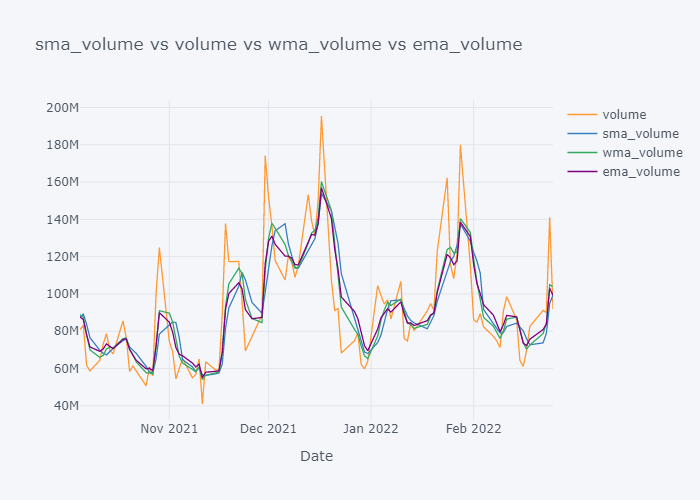
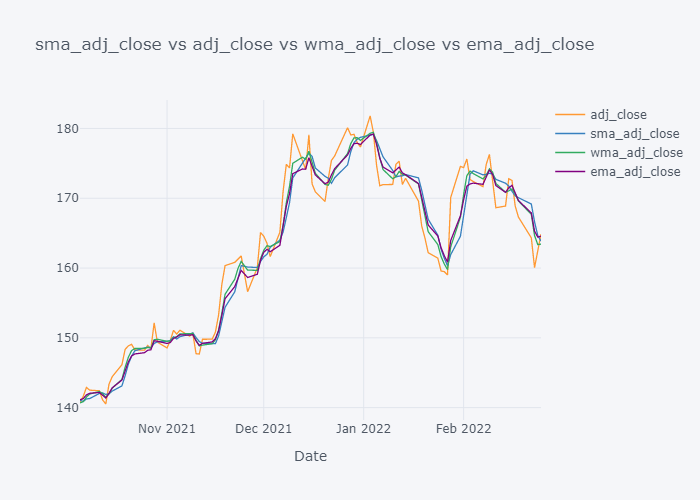
Looking over the EMA,it seems that it is much more smoother than the other values. But the smoothness depends on the value of the smoothing. Based on EMA, lots of other important metrics are calculated in Stock Market Analysis and to note down few:

  • Guppy Moving Average (GMMA)
  • Percentage Price Oscillator (PPO)
  • Relative Strength Index (RSI)
  • Moving Average Convergence Divergence (MCAD)

We will be exploring all above 4 metrics in the next blog please stay tuned for that.

Plotting Candlestick

Candlesticks are often used in stock data analysis for clear visualization and lets try that as well. We will use graph_objects of Plotly.

import plotly.graph_objects as go

fig=go.Figure()

fig.add_trace(go.Candlestick(x=tdf[-1000:].index,
                open=tdf[-1000:]['open'],
                high=tdf[-1000:]['high'],
                low=tdf[-1000:]['low'],
                close=tdf[-1000:]['close'], 
                 name = 'Stock Market Data'))
fig.add_trace(go.Candlestick(x=tdf[-1000:].index,
                open=tdf[-1000:]['ema_open'],
                high=tdf[-1000:]['ema_high'],
                low=tdf[-1000:]['ema_low'],
                close=tdf[-1000:]['ema_close'], 
                 name = 'EMA Stock Market Data'))

fig.update_layout(
    title= "AAPL Stock Data",
    yaxis_title="Stock's Price in USD",
    xaxis_title="Date")               

fig.update_xaxes(
    rangeslider_visible=True,
    rangeselector=dict(
        buttons=list([
            dict(count=150, label="150D", step="day", stepmode="backward"),
            dict(count=4, label="4m", step="month", stepmode="backward"),
            dict(step="all")
        ])
    )
)

color_hi_fill = 'black'
color_hi_line = 'blue'

color_lo_fill = 'yellow'
color_lo_line = 'purple'

fig.data[0].increasing.fillcolor = color_hi_fill
fig.data[0].increasing.line.color = color_hi_line
fig.data[0].decreasing.fillcolor = 'rgba(0,0,0,0)'
fig.data[0].decreasing.line.color = 'rgba(0,0,0,0)'

fig.data[1].increasing.fillcolor = 'rgba(0,0,0,0)'
fig.data[1].increasing.line.color = 'rgba(0,0,0,0)'
fig.data[1].decreasing.fillcolor = color_lo_fill
fig.data[1].decreasing.line.color = color_lo_line

fig.write_image("stock_analysis/candle.png")

fig.show()

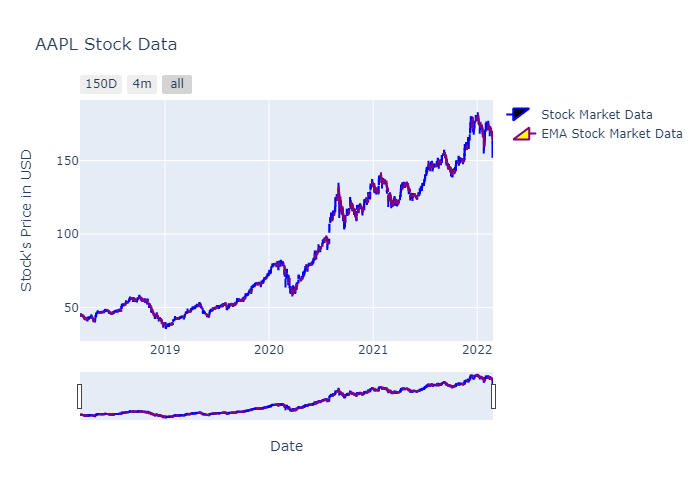
Moving Median

What if we used median instead of the mean? Lets copy and paste the codes written in above steps and calculate median instead of the mean.

tdf = df.copy()
smmdf = tdf.rolling(window=5).median()

for c in smmdf.columns:
    tdf[f"smm_{c}"] = smmdf[c]

emadf=df.ewm(span=5, min_periods=5, adjust=True).mean()

for c in emadf.columns:
    tdf[f"ema_{c}"] = emadf[c]
    
smmc = [c for c in tdf.columns if "smm" in c]
emac = [c for c in tdf.columns if "ema" in c]
col = [c for c in tdf.columns if "smm" not in c and "ema" not in c]

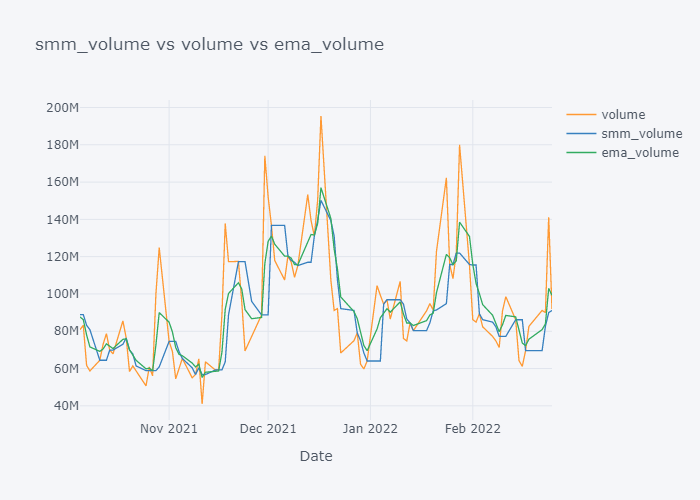
for s,c,e in zip(smmc,col,emac):
    fig=tdf[-100:][[c, s, e]].iplot(kind="line", title=f"{s} vs {c} vs {e}", xTitle="Date", asFigure=True)
    fig.write_image(f"stock_analysis/mma_{c}.png")
    fig.show()

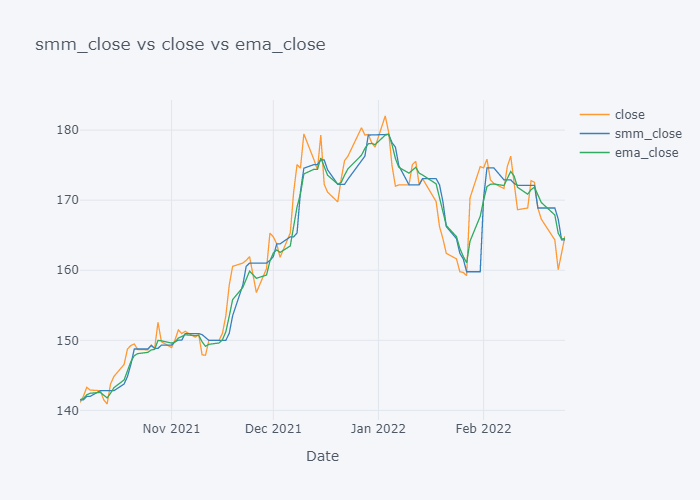
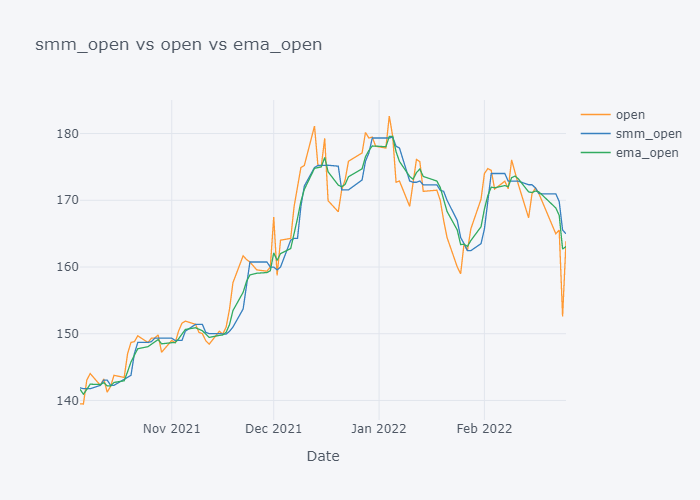
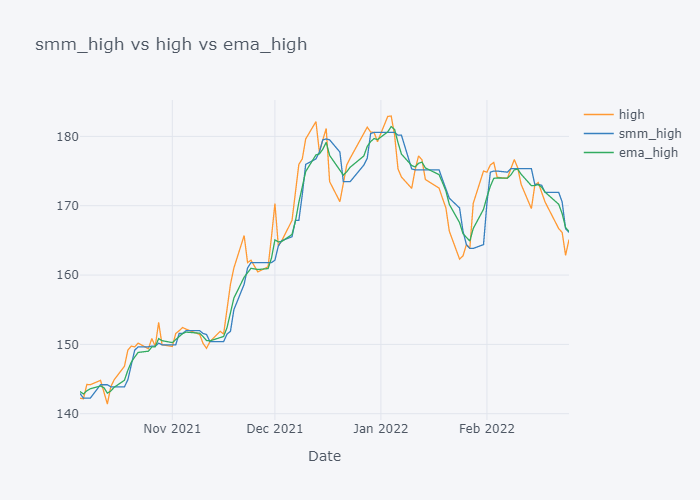
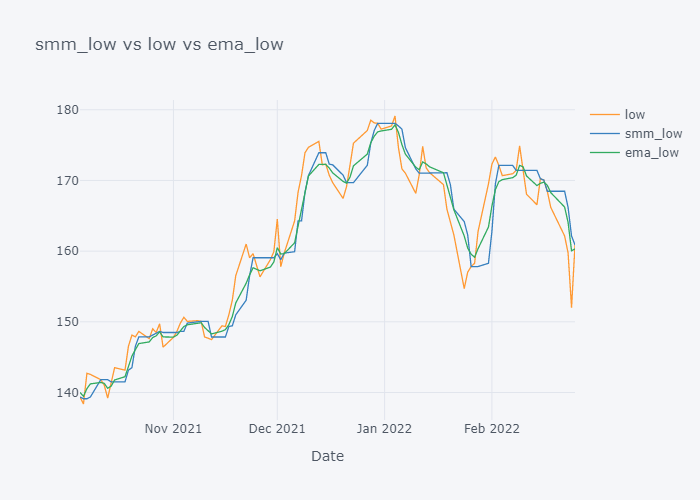
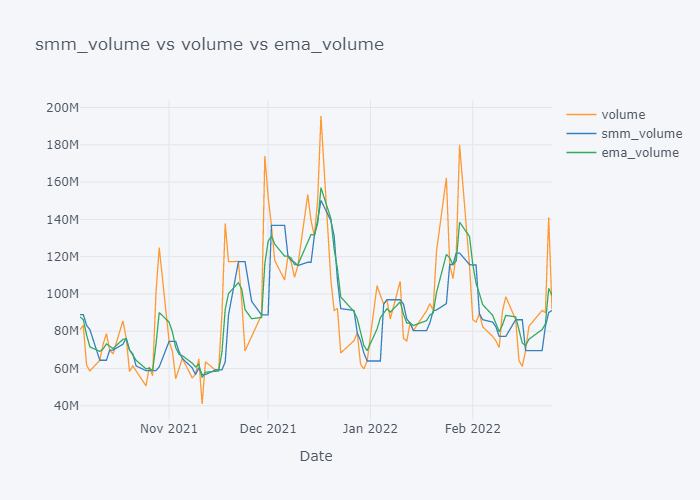
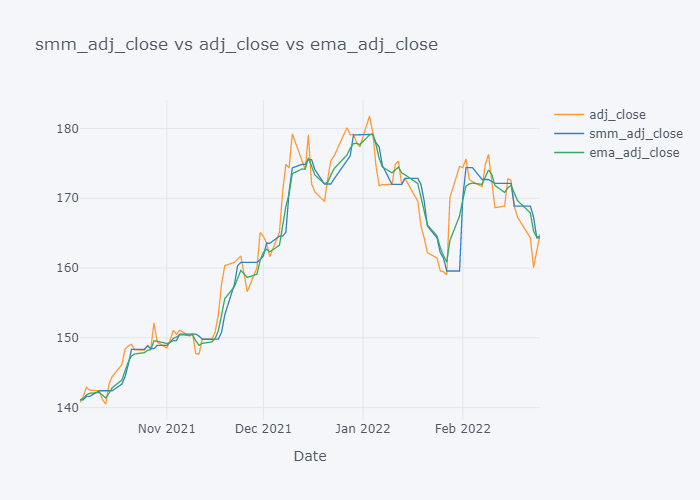
EMA seems to be much near to the open and EMA is more sensitive towards the change than Simple Moving Median.

Moving Variance

tdf = df.copy()
smmdf = tdf.rolling(window=5).var()

for c in smmdf.columns:
    tdf[f"smv_{c}"] = smmdf[c]

emadf=df.ewm(span=5, min_periods=5, adjust=True).var()

for c in emadf.columns:
    tdf[f"emv_{c}"] = emadf[c]
    
smmc = [c for c in tdf.columns if "smv" in c]
emac = [c for c in tdf.columns if "emv" in c]
col = [c for c in tdf.columns if "smv" not in c and "emv" not in c]

for s,c,e in zip(smmc,col,emac):
    fig=tdf[-100:][[c, s, e]].iplot(kind="line", y = [s,e], secondary_y=c, title=f"{s} vs vs {e}", xTitle="Date", asFigure=True)
    fig.write_image(f"stock_analysis/mva_{c}.png")
    fig.show()

Variance seems to be increasing when there is sudden change in the trend and it seems to be decreasing when the change seems to be normal.

Conclusion

In this blog, we have explored some of popular moving average algorithms used in the stock market analysis and in the next blog, we will explore some of the popular metrics that uses Moving Average as the base metric.

References

Comments

You May Also Enjoy

Advent of Code 2022 with Python

4 minute read

The advent of Code is a yearly festival for programmers like me where we try to solve different stories to gain stars. I love these challenge because its fun...

Text Analysis with WordCloud in Python

5 minute read

WordCloud in Python can be done in different ways but one of the most popular and easier ones is using the package wordcloud. We can install it using the fol...

Simple Cryptography Algorithms in Python

2 minute read

Cryptography Algorithms have been around the world for more than centuries and there are still many inscriptions around various places in the world which we ...